UTFPR - Pato Branco - Física 1 - Listas - Teste 9 - Listas Prof. Marcelo Sandrini - Lista 4 - Questão 10
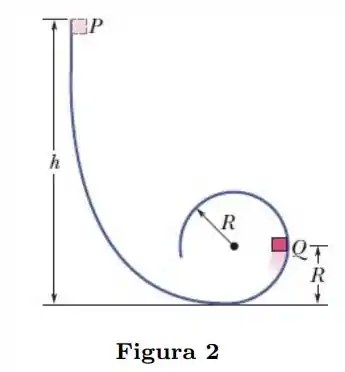
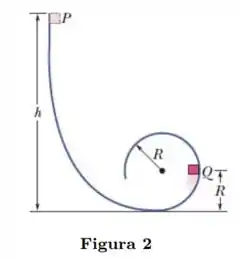
Na Fig. 2 um pequeno bloco de massa pode deslizar em uma pista sem atrito que forma um loop de raio . O bloco é liberado a partir do repouso no ponto , a uma altura acima do ponto mais baixo do loop. Qual é o trabalho realizado sobre o bloco pela força gravitacional enquanto o bloco se desloca do ponto para o ponto e o ponto mais alto do loop? Se a energia potencial gravitacional do sistema bloco-Terra for tomada como nula na base do loop. quanto valerá essa energia potencial quando o bloco estiver no ponto , no ponto e no topo do loop? Se, em vez de ser simplesmente liberado, o bloco recebe uma velocidade inicial dirigida para baixo ao longo da pista, as respostas dos itens de até aumentam, diminuem ou permanecem as mesmas?
Passo 1
Oiie, tudo bem?
Nós temos aqui um bloquinho que parte do repouso a partir de uma altura e segue o seu movimento ao longo de uma pista que termina em um loop de raio . As alternativas e tratam de analisar o trabalho realizado pela força gravitacional para chegar no ponto e no topo do loop. Para isso vamos lembrar que a força gravitacional é uma força conservativa, e portanto, o trabalho realizado pode ser obtido pela seguinte expressão
em que é a energia potencial gravitacional!
As energias potenciais que iremos calcular nas alternativas , e ) requerem a escolha de um referencial, que o problema nos indica como a base do loop sendo o ponto de energia potencial nula. Desta forma, precisamos apenas usar a definição
para calcularmos a energia potencial nos diferentes pontos! Por último, devemos analisar a influência de uma velocidade inicial nos valores obtidos nas questões anteriores! Vamos começar? Vem comigo!
Passo 2
Começando com o trabalho para chegarmos ao ponto , o esquema do loop é o seguinte
Note que o ponto está a uma altura , portanto, como a força gravitacional é conservativa, temos que
Temos que e . De forma que temos que
Substituindo os valores dados no enunciado como e . Obtemos para o trabalho, que
Para o topo do loop, é o mesmo processo, mas temos que agora a altura final será , de forma que temos
e o trabalho resulta em
Note que no processo de resolver a alternativa e utilizamos a energia potencial no ponto e no topo do looping, portanto temos as respostas das alternativas e . Vamos fazer um resumo no próximo passo!
Passo 3
Nós temos que a energia potencial no ponto é dada por
como temos que , temos que a energia potencial é
Analogamente, temos que
e para o topo do loop, temos
Vamos reservar agora o próximo passo para discutir a alternativa . Vem comigo!
Passo 4
Temos que o acréscimo de uma velocidade inicial não afetará em nada os valores calculados até agora, note que as expressões não dependem da velocidade. Mas okay, vamos analisar uma que depende, e ver que é indiferente! O trabalho pode ser obtido através da variação da energia cinética! Ou seja, temos que
No caso em que partimos do repouso, isso equivale à
No caso, em que temos uma velocidade inicial, isso será
No entanto, temos que
já que temos apenas a adição de um termo constante, sem alterar em nada as forças do sistema. Ou seja, na realidade, a condição com velocidade inicial resultará em
Que é o mesmo trabalho obtido originalmente! O trabalho não depende de um fator constante arbitrário, assim como a energia potencial também não depende!