UFPE – Geometria Analítica – 2018.1 – P1 – Questão 1
Seja uma base ortogonal. Calcule o produto escalar entre e .
Passo 1
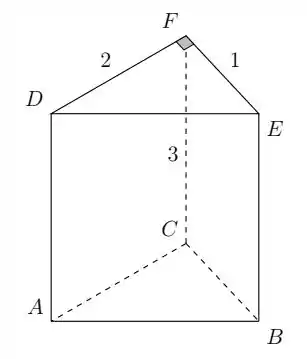
Então, galera, dá uma olhada pra figura. A gente já viu que é uma base ortogonal. Seria bom se a gente tivesse uma base ortonormal pra poder representar os vetores que queremos nessa base! Então a idéia vai ser dividir cada um dos vetores da base ortogonal pelo módulo do vetor da base ortonormal! Vamos criar essa nova base ortonormal.
Passo 2
Pronto, criada a nossa base, já podemos escrever os vetores e nessa base!
Vamos trabalhar em cima do vetor primeiro.
Agora se liga na figura! Percebe que e que ? Então vamos substituir isso:
Vamos pro agora!
Como :
Viu que e ?
Passo 3
Falta só calcular o produto escalar! Essa parte é melzinho na chupeta.
Resposta
Exercícios de Livros Relacionados
6. Em cada parte, decida se o conjunto de matrizes dado é ortogonal em relação ao produto interno M 22 discutido no Exemplo 6 da Seção 6.1.(a) 1 0 0 0 , 0 2 3 1 3 - 2 3 , 0 2 3 - 2 3 1 3 ,0 1 3 2 3 2
7. Em cada parte, mostre que o conjunto de vetores dado é ortogonal com o produto interno euclidiano e converta-o num conjunto ortonormal normalizando os vetores.(a) - 1,2 , 6,3 (b) 1,0 , - 1 , 2,0 ,
Consideremos a seguinte base do R 3 : B = 1 ,0 ,0 ,0 ,1 ,1 ,( 0 ,1 ,2 ) Ortonormalizar essa base pelo processo de Gram-Schmidt, segundo o produto interno usual de cada espaço.
Consideremos a seguinte base do R 2 : B = 3 ,4 ,1 ,2 Ortonormalizar essa base pelo processo de Gram-Schmidt, segundo o produto interno usual de cada espaço.
O conjunto B = 1 2 , 1 2 ,- 1 2 , 1 2 é uma base ortonormal do R 2 com o produto interno usual. Determinar o vetor coordenada de v = ( 2 ,4 ) em relação à base B . Utilizar o processo apresentado em 3