Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Bases Ortogonais e Ortonormais

Ver Teoria
Exercício 1212345678910111314151617181920212223

Enunciado

Seja B = ( i → ,   j → ,   k → ) uma base ortonormal. Sejam u → = 1 ,   1 ,   0 B e v → = 0 ,   1 ,   0 B . Considere os vetores v 1 → , versor de u → , v 2 → versor de v → - P r o j u → v → e v 3 → = v 1 → ∧ v 2 → . Mostre que a sequência ( v 1 → ,   v 2 → ,   v 3 → ) é uma base ortonormal.

(Lembre que o versor de um vetor x → é um vetor unitário com mesma direção e sentido que x → ).

Passo 1

Vamos pensar, o exercício nos deu 3 vetores e quer que a gente prove que eles são uma base ortonormal, ou seja, eles devem ser ortogonais entre si e ter módulo 1.

Primeiro vamos ver a ortogonalidade beleza?

Seja um vetor w → e um vetor z → . Pela definição de projeção ortogonal, a gente sabe que w → e z → - P r o j w → z → são ortogonais, olha:

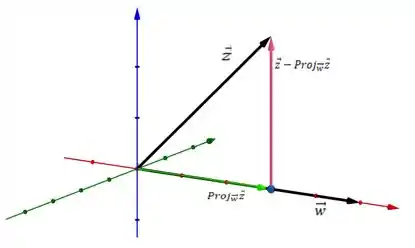
Sacou??

Então analogamente a isso, a gente sabe que u → e v → - P r o j u v → são ortogonais, logo v 1 → e v 2 → (que são seus versores) são ortogonais :P

Ta mas e v 3 → ?

Ele é o produto vetorial de v 1 → com v 2 → , e a gente sabe que o produto vetorial sempre vai ser um terceiro vetor ortogonal aos outros 2 né? Então fechouuu, já sabemos que v 1 → , v 2 → e v 3 → são ortogonais entre si!!

Passo 2

Agora vamos ver se esses vetores são unitários.

Olha, a gente sabe que v 1 → e v 2 → são versores, então pela definição de versor já temos que eles são unitários!!

O módulo de v 3 → , pela definição de produto vetorial, é dado assim:

v 3 → = v 1 → ∧ v 2 → = v 1 → . v 2 → . s e n θ

v 3 → = 1 . 1 . s e n 90 °

v 3 → = 1

Aeee então v 3 → também é unitário!!

Logo, a sequência ( v 1 → ,   v 2 → ,   v 3 → ) é formada por vetores ortogonais entre si e unitários, portanto é uma base ortonormal :)

Resposta

Demonstração.

Exercícios de Livros Relacionados

6. Em cada parte, decida se o conjunto de matrizes dado é ortogonal em relação ao produto interno M 22 discutido no Exemplo 6 da Seção 6.1.(a) 1 0 0 0 , 0 2 3 1 3 - 2 3 , 0 2 3 - 2 3 1 3 ,0 1 3 2 3 2
7. Em cada parte, mostre que o conjunto de vetores dado é ortogonal com o produto interno euclidiano e converta-o num conjunto ortonormal normalizando os vetores.(a) - 1,2 , 6,3 (b) 1,0 , - 1 , 2,0 ,
Consideremos a seguinte base do R 3 : B = 1 ,0 ,0 ,0 ,1 ,1 ,( 0 ,1 ,2 ) Ortonormalizar essa base pelo processo de Gram-Schmidt, segundo o produto interno usual de cada espaço.
Consideremos a seguinte base do R 2 : B = 3 ,4 ,1 ,2 Ortonormalizar essa base pelo processo de Gram-Schmidt, segundo o produto interno usual de cada espaço.
O conjunto B = 1 2 , 1 2 ,- 1 2 , 1 2 é uma base ortonormal do R 2 com o produto interno usual. Determinar o vetor coordenada de v = ( 2 ,4 ) em relação à base B . Utilizar o processo apresentado em 3