Um elétron é projetado com velocidade inicial para dentro do campo elétrico uniforme entre as placas paralelas indicadas na figura abaixo. Suponha que o campo seja uniforme e orientado verticalmente para baixo e considere igual a zero o campo elétrico fora das placas e despreze a força peso. O elétron entra no campo em um ponto intermediário entre as placas.
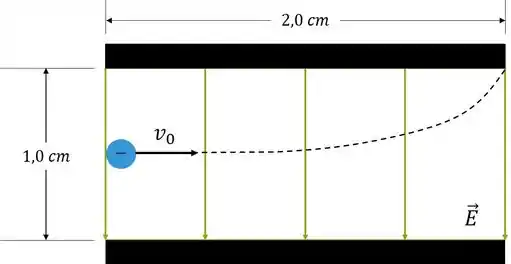
- Sabendo que o elétron tangencia a placa superior quando ele sai do campo, calcule o módulo do campo elétrico;
Dados:
Passo 1
O começo da questão é um problema de cinemática. O elétron tangenciar a placa ao sair do campo implica que o deslocamento em é igual à:
Ao passo que o deslocamento em é:
Para a componente temos um movimento de velocidade constante:
Tendo a velocidade e o deslocamento, isolamos o tempo e substituímos os valores:
Passo 2
Nesse mesmo intervalo de tempo o elétron viajou verticalmente, só que num movimento acelerado proveniente do campo elétrico. Vamos desprezar efeitos da gravidade pois a massa do elétron é muito pequena, já é?
Para a componente :
Temos o deslocamento e o intervalo de tempo.
Como inicialmente o elétron se desloca na direção horizontal a sua velocidade vertical inicial é nula
Daí segue que:
Show. Podemos inferir o valor do campo à partir da aceleração!
Passo 3
Como temos que:
E temos a aceleração e a massa (a massa do elétron é tabelada)! Podemos então descobrir o valor do campo, por conta da fórmula:
Partiu então. Como só queremos o módulo (direção e sentido já foram dadas no enunciado) vamos trabalhar só com ele mesmo:
Substituindo os valores (lembrando que a carga do elétron é tabelada também):
Finalmente!