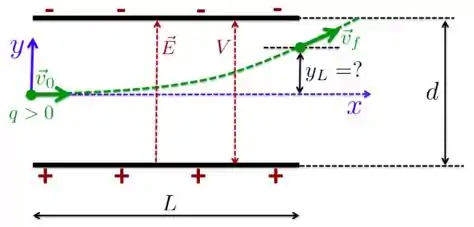
Uma carga positiva , com velocidade , entra na região entre duas placas paralelas numa direção perpendicular a um campo elétrico uniforme . As placas são separadas por um distância e submetidas a uma diferença de potencial , como indicado na Figura abaixo. A carga percorre todo o espaço entre as placas e sai dessa região com uma velocidade , inclinada em relação ao eixo e a uma distância desse eixo. Desprezando a força gravitacional, qual o valor da posição ? Expresse seu resultado em termos de , , , e .
Passo 1
Aqui temos uma carga positiva que entra numa região onde há um campo elétrico uniforme e apontando na direção de . Nesse caso, a carga positiva vai sentir uma força de atração em direção às placas negativas e essa força vai ter a mesma direção, sentido e módulo ao longo de todo o seu percurso no interior das placas. Blz quanto a isso?
Bom, como estamos desconsiderando a força gravitacional sobre a carga, então, da segunda lei de Newton, a gente tem o seguinte valor para a aceleração na direção :
Por outro lado, se a gente olha agora para a direção do eixo , a carga não tem aceleração, ou seja, a carga positiva tem um movimento com velocidade uniforme na direção . Isso significa que ao longo do eixo , a velocidade da partícula será sempre . Sacou?
Agora, olha só, a gente tem a mesma situação que lá no caso do movimento oblíquo de uma partícula lançada na presença de um campo gravitacional. Por isso, aqui no caso da Figura acima, a partícula carga também vai descrever uma trajetória parabólica na região dentro das placas!! IMPORTANTÍSSIMO ISSO…GUARDA AÍ COM CARINHO NO CORAÇÃO…
Tamo junto até aqui?? Segue firme comigo…
Passo 2
Como o movimento é uniformemente acelerado na direção , a equação horária para posição é
sendo que é a velocidade inicial da carga na direção . Lembrou disso?
Bom, o que a gente quer é encontrar , correto? Mas, da Figura, vemos que a posição e velocidade inicial, ambas em , são:
Substituindo isso e lembrando da expressão para a aceleração, que é , obtemos que
Tranquilo? Precisamos, agora, só colocar essa expressão em termos das quantidades pedidas pelo exercício. Vamos lá?
Passo 3
Como o movimento da carga na direção é uniforme, podemos encontrar o tempo que ela gasta para percorrer o comprimento das placas. Portanto,
Esse tempo é exatamente o mesmo tempo que a carga gasta para percorrer, na direção , a distância , blz? Por isso, a gente vai usar esse tempo lá na expressão para daqui um pouco...
Além disso, o módulo do campo elétrico uniforme se relaciona com a diferença de potencial e a distância entre as placas paralelas da seguinte maneira:
Substituindo essas duas últimas expressões naquela do Passo 2 para , obtemos:
OK? Esse exercício é interessante porque faz um paralelo direto com o caso gravitacional do lançamento oblíquo que você viu lá na Física 1 e, da mesma maneira que lá naquele caso, a gente tem aqui também uma partícula de massa , porém carregada, descrevendo uma trajetória parabólica.