UFRJ, Sem Campus, Física 3, Listas de Física 3 - UFRJ - Lista 1 - Carga Elétrica e Campo Elétrico, Questão 8b
Uma linha isolante de cargas tem a forma de um semicírculo de raio , como indicado na figura abaixo. Sua densidade linear de carga é dada por , onde é uma constante positiva e é o ângulo polar medido a partir do eixo .
(b) Determine o vetor campo elétrico no centro do semicírculo.
Passo 1
Eaee!!! Belezinha? Bom... a questão nos pede para calcular o vetor campo elétrico no centro do semicírculo, ou seja, o campo elétrico no ponto :
Para isso, primeiro temos que analisar o comportamento dos elementos infinitesimais que compõem a linha. Veja a figura abaixo
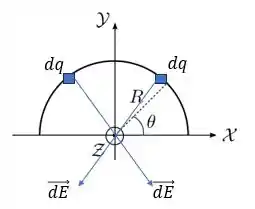
Perceba que sempre haverá um componente simétrico de e, portanto, de .
Dessa forma, se arrastarmos em torno da linha, veremos apenas um campo resultante apontando para baixo.
Assim, podemos ignorar as componentes horizontais da linha de cargas e trabalhar apenas com as componentes verticais de tal forma que:
E aí? Bora lá desenvolver??!!
😉
Passo 2
Assim, sabemos que o diferencial de campo elétrico é dado por:
Onde . Portanto:
Assim, aplicando em , temos:
Integrando no semicírculo, temos:
Utilizando a identidade trigonométrica , temos:
Entendeu direitinho? Responde aee ;)
