Duas minúsculas bolas de massa possuem carga de módulo , porém de sinais contrários. Elas estão atadas ao mesmo gancho de teto por fios leves, de comprimento . Quando um campo elétrico uniforme horizontal é ativado, as bolas ficam suspensas a um ângulo entre os fios, como mostra a Figura abaixo. Considere que o campo elétrico seja intenso suficiente para que a força eletrostática entre as cargas e possa ser desconsiderada.
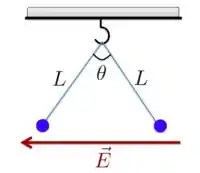
- Qual bola (a da esquerda ou a da direita) é positiva e qual é negativa?
- Ache o ângulo entre os fios em termos de , , e ;
- À medida que a intensidade do campo elétrico aumenta, o que o resultado do item b) fornece para o maior ângulo possível?
Passo 1
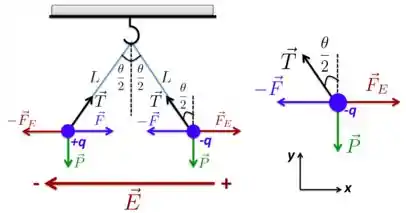
a) Aqui é importante que a gente se lembre de que o campo elétrico sempre aponta das cargas positivas para as cargas negativas, como mostra a Figura abaixo. Portanto, a carga positiva se aproxima da região onde se encontra a região negativa do e a carga negativa da região positiva desse mesmo campo. Tranquilo?
Passo 2
b) Dada essa situação, na Figura acima, mostro para você como ficam os vetores das forças que atuam sobre as cargas e . Na direita da figura, a gente tem a carga isolada com as forças que atuam sobre ela representadas.
Como esta carga está em equilíbrio, a soma das forças na direção e devem ser iguais, o que dá para gente o seguinte sistema de equações:
Agora, como o enunciado diz que o campo é intenso o suficiente para que a gente despreze a força de Coulomb entre as cargas puntiformes e comparado com a força que atua nelas, podemos reescrever as componentes das forças em e como
Se a gente divide a primeira equação acima pela segunda expressão, chegamos a
Passo 3
c) Agora, a partir da expressão acima para o ângulo em função do módulo do campo , repara que a gente tem os seguintes comportamentos:
- ,
já que, quando . Isso significa que, quanto mais intenso o campo elétrico, mais o ângulo entre os dois fios se aproxima de e, com esse ângulo, os fios vão estar alinhados e as cargas estarão encostadas no teto e separadas por uma distância .
Resposta
- Carga da esquerda é positiva e a da direita negativa;
- À medida que aumenta, aumenta e, para , .