UFSC, Sem Campus, Física 3, Provas de Física 3 - Profº Abílio - 1ª Avaliação Parcial (P1), Questão 1
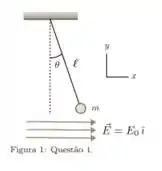
Uma pequena esfera carregada de massa m e carga está suspensa por um fio leve de comprimento , conforme mostra a Figura 1. Um campo elétrico uniforme é aplicado na direção x, onde é uma constante positiva. Obtenha uma expressão para a carga elétrica da esfera em função do ângulo θ que ela forma com a vertical quando ela está em equilíbrio. (Considere a aproximação para ângulos pequenos tan θ ≈ sen θ ≈ θ).
Passo 1
Eaew, belezinha?
Temos que obter uma expressão para a carga elétrica da esfera em função do ângulo θ que ela forma com a vertical quando ela está em equilíbrio. Temos que lembrar que no equilíbrio a força resultante é nula. Então, se somarmos as forças atuando nas direções x e y, o resultado deve ser zero. Então, vamos construir o diagrama de forças e obter uma relação para essas duas direções.
Então vamos lá!
Passo 2
Primeiro vamos identificar quais forças atuam sobre a massa. Temos a força peso na vertical, a força elétrica na horizontal, e a força de tração na diagonal.
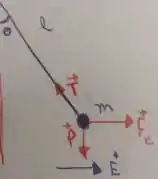
Podemos escrever essas forças da seguinte forma:
Passo 3
Assim, escrevendo a força resultante em cada direção, temos:
Então,
Substituindo na resultante de y:
Considerando a aproximação para ângulos pequenos tan θ ≈ sen θ ≈ θ:
.
A questão foi isso! Te vejo na próxima! Tchau Tchau!
Resposta
.