Unicamp, Física 3, 2019.2, P1, Questão 4.
Uma haste rígida isolante, com duas cargas de sinal oposto e módulos diferentes presas às suas extremidades, é colocada em um campo elétrico uniforme , como mostrado. A haste sofre:
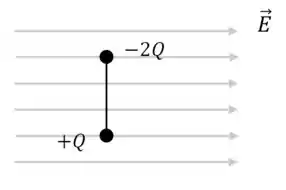
a) uma força resultante para a esquerda e uma rotação no sentido horário
b) uma força resultante para a esquerda e uma rotação no sentido anti-horário
c) uma força resultante para a direita e uma rotação no sentido horário
d) uma força resultante para a direita e uma rotação no sentido anti-horário.
e) uma força resultante nula e uma rotação no sentido antihorário.
Passo 1
Vamos começar lembrando da fórmula que dá a força que uma carga sofre em um campo elétrico:
Isso quer dizer que a força na parte de cima da haste é:
O sinal negativo diz que a força aponta no sentido contrário ao campo.
E a força na parte de baixo da haste é:
E dessa vez a força aponta no mesmo sentido do campo.
Vamos representar isso no desenho:
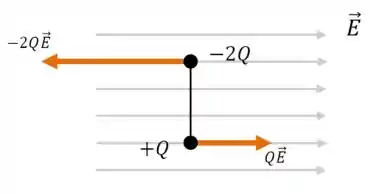
Passo 2
Então vamos ver o que acontece com a força resultante:
Ou seja, temos uma força resultante! E ela aponta na direção oposta ao campo, portanto para a esquerda.
E a rotação? Bom, pra isso é só olhar o desenho. As duas forças favorecem a rotação no sentido anti-horário:
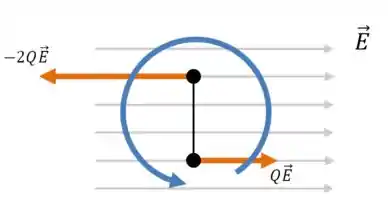
Ou seja, a resposta correta é a alternativa (b).
Resposta
Alternativa (b).