UFRJ – Física 3 2020.2 – P2 – Questão 1
Três placas infinitas com densidade superficial de carga elétrica são mostradas na figura abaixo:
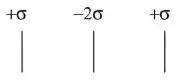
A placa central possui densidade superficial de carga negativa , enquanto que as duas placas laterais possuem densidade superficial de carga positiva . Se representarmos a direção e sentido do campo elétrico em cada uma das regiões separadas pelas placas infinitas, qual é o conjunto de setas que melhor representa sua configuração?
Escolha uma:
Passo 1
Fala galera, tudo bem? Supondo que a placa mais à esquerda produza um campo representado em azul, a placa do meio em vermelho e a mais à direita em verde, o desenho desses campos está aqui:
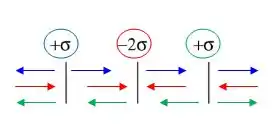
Lembrando que placas positivas produzem campos “saindo”, enquanto que placas negativas produzem campos “entrando”.
O campo produzido por uma placa é:
Para determinar o valor do campo em cada região, precisamos somar as contribuições das três placas.
Beleza até aqui?
Passo 2
Os campos produzidos pelas placas são:
Para saber o sentido de cada campo em cada região, é só dar uma espiadela no desenho do passo anterior.
A região à esquerda da placa azul:
A região entre as placas azul e vermelha:
Entre as placas vermelha e verde:
E à direita da placa verde:
Passo 3
Sendo assim, o campo entre as placas é:
Analisando as alternativas, a correta é a (e).