Cargas Elétricas, Forças Elétricas, Campo Elétrico
Duas pequenas esferas carregadas, cada uma de massa , estão suspensas por fios de comprimento , conforme diagrama abaixo. Um campo elétrico uniforme e aplicado ao longo da direção . As esferas possuem cargas iguais a e .
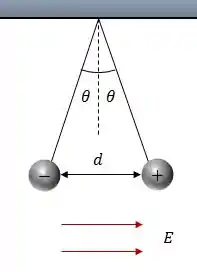
Determine:
A força elétrica em função de e , sobre cada esfera de modo que o conjunto fique em equilíbrio;
O campo elétrico nas mesmas condições dadas no item ;
A tensão no fio nas mesmas condições dadas no item ;
Passo 1
A força elétrica em função de e , sobre cada esfera de modo que o conjunto fique em equilíbrio;
A primeira coisa aqui é fazer o diagrama de corpo livre pra dar uma olhada na situação:
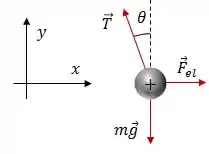
Como o sistema está em equilíbrio, podemos dizer que:
A partir da segunda equação, podemos escrever:
Substituindo isso na primeira equação, teremos:
Passo 2
O campo elétrico nas mesmas condições dadas no item ;
Agora precisamos encontrar uma nova expressão para a força elétrica:
A força elétrica resultante sobre cada esfera será a soma vetorial da força elétrica de interação entre as duas esferas e a força elétrica exercida pelo campo elétrico externo.
De acordo com a geometria do problema, podemos dizer que:
Logo:
Finalmente:
Passo 3
Igualando as expressões do passo e do passo para isolar o campo elétrico...
Pra terminar com isso, só falta isolar o e arrumar a bagunça:
Finalmente:
Passo 4
A tensão no fio nas mesmas condições dadas no item ;
Podemos escrever duas expressões para a tensão no fio. Nós escrevemos essas duas expressões no passo anterior. São elas:
e
Resposta