Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Campo Magnético Gerado por uma Bobina

Ver Teoria
Exercício 32123456789101112131415161718192021222324252627282930313334353637383940

Enunciado

Física 2 - UFF; P2 de 2019.2

13 - Para que uma determinada engenhoca funcione corretamente é necessário que uma bobina de raio R = 1,0 c m transportando uma corrente de 100 ,   0   μ A   seja imersa em um campo magnético constante B   =   2 ,   0   π   μ T . Contudo, também é necessário que o campo magnético no centro da bobina seja nulo. Para isso, precisamos garantir que:

  1. O campo magnético produzido pela bobina esteja alinhado paralelamente ao campo magnético B e que a bobina possua 10 3 espiras.
  2. O campo magnético produzido pela bobina seja transversal ao campo magnético B e que a bobina possua 10 3 espiras.
  3. O campo magnético produzido pela bobina esteja alinhado antiparalelamente ao campo magnético B e que a bobina possua 10 3 espiras.
  4. O campo magnético produzido pela bobina esteja alinhado paralelamente ao campo magnético B e que a bobina possua 10 5 espiras.
  5. O campo magnético produzido pela bobina esteja alinhado antiparalelamente ao campo magnético B e que a bobina possua 10 5 espiras.

Passo 1

Uma bobina, nada mais é do que um aglomerado de n espiras que quando possui uma corrente girando nela, produz um campo paralelo como o da figura:

O campo magnético B b o b i n a de uma bobina é então n vezes mais o campo de uma espira:

B b o b i n a = n μ 0 i R 2 2 z 2 + R 2 3 / 2

Onde z é a posição do ponto onde estamos medindo o campo magnético da bobina. Se estivermos falando de um ponto interior (como é o caso do problema): z = 0 . Então...

B b o b i n a = n μ 0 i R 2 2 R 2 3 2 =

n μ 0 i R 2 2 R 3

Ou seja...

B b o b i n a = n μ 0 i 2 R

Passo 2

Queremos que o campo no interior da bobina seja nulo, então a primeira coisa a fazer é posicionar o campo B B o b i n a contra o campo B que do meio:

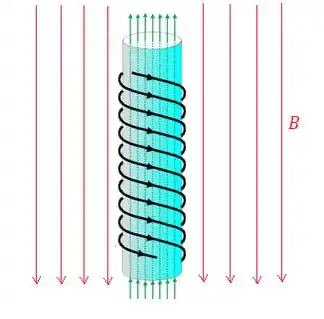
Isso significa estar antiparalelo com o campo B externo.

Passo 3

Quanto ao número n de espiras necessário, podemos tirar aqui:

B b o b i n a = n μ 0 i 2 R

Para o campo magnético ser nulo no interior, além de estar alinhados como no passo anterior, os módulos dos campos (da bobina e externo) devem ser iguais! Assim, como o campo externo é B =   2 ,   0   π   μ T , então...

B b o b i n a =   2 ,   0   π   μ T

Sendo a corrente i = 100   μ A , o raio R = 1   c m (ou 0,01   m ) e ainda...

μ 0 = 4 π ⋅ 10 - 7     T m / A

Então...

B b o b i n a = n μ 0 i 2 R   →

n = 2 R ⋅ B b o b i n a μ 0 i   →

n = 2 0,01 ⋅ 2 ,   0   π 4 π ⋅ 10 - 7 100   →

n = 0,01 10 - 7 100 =

1000 = 10 3

Resposta

Letra C.

Exercícios de Livros Relacionados

79- Uma bobina de alto-falante. Na seção 27.7 , mostramos que era igual a zero a força resultante sobre uma espira de corrente em um campo magnético uniforme. A força magnética sobre uma bobina destin
87- Uso da Lei de Gauss do magnetismo. Em uma certa região do espaço, o campo magnético B → não é uniforme. O campo magnético possui um componente z e outro componente que aponta para fora ou para den
Um solenóide de comprimento 30 cm, raio 1,2 cm e 300 voltas, conduz corrente de 2,6 A. Determine a magnitude do campo magnético no eixo do solenóide:a) No centro do solenóide.b) Em uma extremidade do
Um solenóide tem n voltas por unidade de comprimento, raio R e conduz uma corrente I. Seu eixo coincide com o eixo z – uma extremidade em z = - 1 2 l e a outra em z = + 1 2 l . Mostre que a magnitude
Um único anel condutor tem raio igual a 3,0c m e conduz corrente igual a 2,6A . Qual é a magnitude do campo magnético na linha que passa pelo centro do anel e é perpendicular ao plano do anel a No cen