UFRJ – Física 3 – 2020.2 – P5 – Exercício 11
Um fio fino circular, de raio , é percorrido por uma corrente estacionária de intensidade . No mesmo plano, temos um outro fio, constituído por dois segmentos retilíneos, longos e um arco de semicircunferência, concêntrico com o primeiro fio, de raio , conforme mostra a figura.
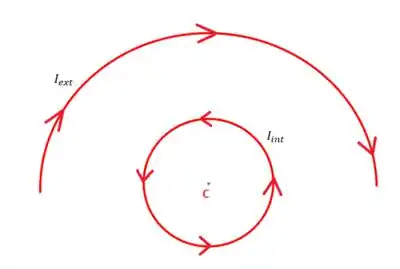
Qual deve ser a intensidade da corrente estacionária , nesse segundo fio, para que o campo magnético no centro comum seja nulo?
a)
b)
c)
d)
e)
Passo 1
Fala galerinha, beleza?
Para resolver esse problema você precisa lembrar de duas coisinhas. A primeira é a expressão do campo magnético produzido por uma espira circular de raio no centro dela:
A segunda, é a fórmula do campo produzido por um arco de espira circular de raio e ângulo :
No caso da semicircunferência, temos :
Passo 2
Na situação do problema, o campo produzido pela espira de dentro é
Já o campo produzido pela semicircunferência de fora é
Bom, estamos quase finalizando o problema!
Olhando os sentidos das correntes, é fácil ver que um desses campos aponta para dentro da tela e o outro para fora. Para que o campo resultante se anule, forçamos
Assim,
Simplificando o que dá para simplificar, achamos
Isso nos leva para a alternativa A 😊.
Resposta
Alternativa A.