Considere um toroide com espiras de raio interno e raio externo (ver figura). Cada espira é percorrida por uma corrente elétrica .
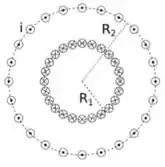
a) Determine o módulo do campo magnético no interior do toroide, i.e., para .
b) Se colocarmos no centro do toroide um fio longo e retilíneo, colinear com o eixo do toroide, qual é a intensidade e sentido da elétrica no fio que anulará o campo magnético no interior do toroide?
Passo 1
Fala galerinha, broca brincar um pouco com campos magnéticos?
No problema temos um toroide com várias espiras e raio interno e raio externo .No item (a) queremos achar o campo magnético no interior do toroide.
Para resolver esse problema, vamos lembrar primeiro do campo magnético no interior de um solenoide:
onde é o número de espiras e o comprimento do solenoide. Vale ressaltar que esse campo é uniforme!
Agora vem o pulo do gato: se a gente torcer o solenoide e juntar suas extremidades nós obtemos o toroide! Com isso, o campo dentro do toroide também será uniforme e dado por
Mas nesse caso, quem é o ? Podemos pensar nesse comprimento como o comprimento de um círculo:
Mas que raio é esse? Podemos tomar a média entre e :
Assim,
Esse campo será uniforme, porém sua direção será tangencial, de modo que “faz a curva” assim como o toroide. A seguir representamos a linha de campo:
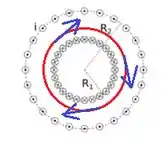
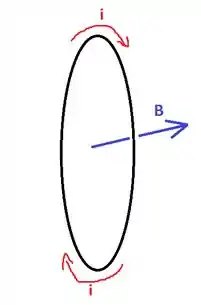
O sentido é esse pela regra da mão direita:
Passo 2
Agora vamos para o item (b). O enunciado diz que um fio infinito é colocado no centro do toroide. Queremos saber qual deve ser a corrente no fio e o sentido dela para que o campo produzido por ela anule o campo do toroide.
Vimos no passo 1 que o campo do toroide gira no sentido horário. Assim, o campo produzido pelo fio deve girar no sentido anti-horário para que eles possam se cancelar:
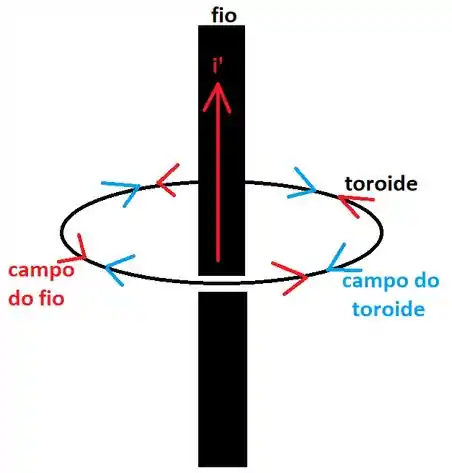
O campo a uma distância do fio é dado por
Usando , de modo que
Passo 3
Para que os campos se anulem, devemos ter
Portanto, a corrente no fio deve ser para cima e seu valor deve ser
Isso significa que a corrente do fio deve ser igual a soma das correntes em cada espira do toroide. O sentido deve ser para cima para que o campo produzido esteja no sentido anti-horário e possa anular o campo do toroide!
Com isso terminamos o problema 😊.