UFJF – Física 3 – AV3 – 2ª CH – 2016.2 – Questão 2c
Uma bobina de espiras foi enrolada num corpo toroidal de raio interno , raio externo e altura , como indica a figura ao lado.
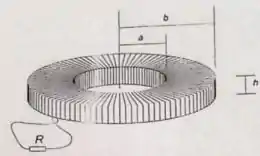
- Os dois extremos do fio enrolado foram conectados com a ajuda de um resistor como mostra a figura. Desta maneira se formou um circuito . A resistência (incluindo a resistência do próprio fio) vale . Com a ajuda da lei de indução foi criada uma corrente neste circuito de tal maneira que em flui uma corrente de . A partir deste instante, o circuito foi deixado sem influência externa. Supondo que , e e calcule em quanto tempo a corrente no circuito diminui para o valor de . Dado: .
Passo 1
Eaee!!! Belezinha? Bom... a questão nos dá uma bobina em formato toroidal em série com uma resistência e nos pede para calcular em o tempo para que a corrente no circuito diminua de para .
Para isso, temos que lembrar que, como o circuito não recebe influência externa, podemos determinar o tempo pela expressão abaixo:
Onde é a corrente, é a corrente inicial, é a resistência, é a indutância e é o tempo.
Essa fórmula é a resposta natural de um circuito
E aí? Bora responder?
Passo 2
Bom... substituindo os dados do enunciado, podemos determinar a indutância da bobina pela fórmula que descobrimos no item b):
Passo 3
Assim, sabendo que , , e , podemos calcular o tempo para que a corrente seja de , ou seja:
Entendeu direitinho? Responde aee ;)
