Exercícios Resolvidos de Campo Magnético Gerado por uma Bobina

Ver Teoria

Exercício 8 1 2 3 4 5 6 7 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40

Enunciado

A figura abaixo mostra um dispositivo conhecido como bobina de Helmholtz, formado por duas bobinas circulares coaxiais de raio , com espiras, separadas por uma distância . As duas bobinas conduzem correntes iguais no mesmo sentido. Determine o módulo do campo magnético no ponto , situado sobre o eixo das bobinas, a meio caminho entre elas.

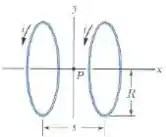
Dados:

Passo 1

Então, galera! Temos duas bobinas de 200 espiras, com correntes iguais e mesmo raio . Queremos saber o campo magnético num ponto P que equidista, ou seja, está a mesma distância das duas bobinas.

Passo 2

Sabemos que o campo magnético gerado por uma bobina de uma espira num ponto a uma distância é dado por:

Como as correntes têm o mesmo sentido, as duas bobinas produzem campos iguais com o mesmo sentido (pela regra da mão direita, encontramos que é o sentido .

Assim, passando para as unidades SI:

Resposta

Exercícios de Livros Relacionados

79- Uma bobina de alto-falante. Na seção 27.7 , mostramos que era igual a zero a força resultante sobre uma espira de corrente em um campo magnético uniforme. A força magnética sobre uma bobina destin

87- Uso da Lei de Gauss do magnetismo. Em uma certa região do espaço, o campo magnético B → não é uniforme. O campo magnético possui um componente z e outro componente que aponta para fora ou para den

Um solenóide de comprimento 30 cm, raio 1,2 cm e 300 voltas, conduz corrente de 2,6 A. Determine a magnitude do campo magnético no eixo do solenóide:a) No centro do solenóide.b) Em uma extremidade do

Um solenóide tem n voltas por unidade de comprimento, raio R e conduz uma corrente I. Seu eixo coincide com o eixo z – uma extremidade em z = - 1 2 l e a outra em z = + 1 2 l . Mostre que a magnitude

Um único anel condutor tem raio igual a 3,0c m e conduz corrente igual a 2,6A . Qual é a magnitude do campo magnético na linha que passa pelo centro do anel e é perpendicular ao plano do anel a No cen