Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Campo Magnético Gerado por uma Bobina

Ver Teoria
Exercício 38123456789101112131415161718192021222324252627282930313233343536373940

Enunciado

A figura abaixo mostra a seção reta de um cilindro com uma cavidade vazia de raio interno a   =   5   c m e raio externo b   =   7   c m . Uma densidade de corrente uniforme J   =   1   A / c m 2 passa pelo cilindro. Com essas informações, qual é a intensidade do campo magnético em um ponto a uma distância d   =   10   c m do eixo do cilindro como destacado na figura?

  1. 0
  2. 1,5 × 10 - 4   T
  3. 2,5 × 10 - 4   T
  4. 4,5 × 10 - 4   T
  5. 0,5 × 10 - 4   T

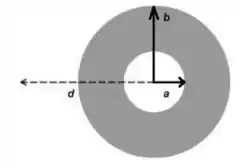
Passo 1

POW! Sabemos da teoria que o campo magnético fora de um cilindro se comporta como um campo magnético de um fio de corrente passando pelo centro do cilindro...

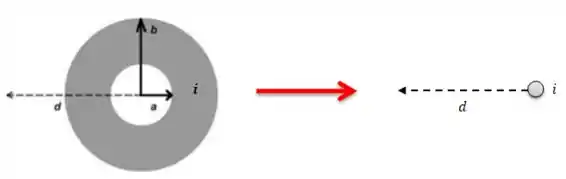
Então... Para encontrar o valor do campo B a uma distância d , podemos usar...

B = μ 0 i 2 π d

Onde i é a corrente que passa no cilindro. Mas quem é essa corrente?

Passo 2

POW! Não conhecemos diretamente a corrente que passa no cilindro, mas conhecemos a densidade de corrente J :

J = 1   A / c m 2

A densidade de corrente pode ser dada por...

J = i A r e a

Onde A r e a representa a área da seção de onde a corrente está sendo transportada. Nesse caso...

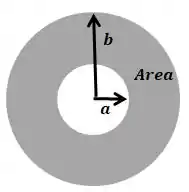
Podemos encontrar o valor dessa área por...

A r e a = π b 2 - π a 2   →

A r e a = π b 2 - a 2

Então...

J = i π b 2 - a 2   →

i = J π b 2 - a 2

Passo 3

Então, finalmente podemos voltar para o cálculo do campo magnético B ...

B = μ 0 i 2 π d   →

B = μ 0 J π b 2 - a 2 2 π d     →

Simplificando...

B = μ 0 J b 2 - a 2 2 d  

Substituindo então os valores dados no enunciado já que b = 7   c m e a = 5   c m ...

B = μ 0 1   A / c m 2 7 2 c m 2 - 5 2   c m 2 2 d     →

B = μ 0 1   A / c m 2 24   c m 2 2 d     →

B = μ 0   24   A 2 d     →

POW! d = 10   c m = 0,1 m (temos que converter para metro, afinal temos que ter as unidades no SI). OBS: o motivo de não termos convertido a e b foi por causa da densidade de corrente que foi dada em A / c m 2 , de modo que conseguimos cortar c m 2 com c m 2 , saca? Mas o d não tem desculpa...

B = μ 0   24   A 2 0,1   m     →

O valor de μ 0 = 4 π ⋅ 10 - 7   T m / A ...

B = 4 π ⋅ 10 - 7 T m A ⋅   24   A 2 0,1   m     →

Simplificando as unidades (cortando m com m e A com A )...

B = 4 π ⋅ 10 - 7   ⋅   12   0,1     T →

B = 4 π ⋅ 10 - 7   ⋅   120     T →

Simplificando mais um pouco tomando π ≅ 3 ...

B = 10 - 7   ⋅   1440     T →

B = 1,44 ⋅ 10 - 4       T

Resposta

Letra B.

Exercícios de Livros Relacionados

79- Uma bobina de alto-falante. Na seção 27.7 , mostramos que era igual a zero a força resultante sobre uma espira de corrente em um campo magnético uniforme. A força magnética sobre uma bobina destin
87- Uso da Lei de Gauss do magnetismo. Em uma certa região do espaço, o campo magnético B → não é uniforme. O campo magnético possui um componente z e outro componente que aponta para fora ou para den
Um solenóide de comprimento 30 cm, raio 1,2 cm e 300 voltas, conduz corrente de 2,6 A. Determine a magnitude do campo magnético no eixo do solenóide:a) No centro do solenóide.b) Em uma extremidade do
Um solenóide tem n voltas por unidade de comprimento, raio R e conduz uma corrente I. Seu eixo coincide com o eixo z – uma extremidade em z = - 1 2 l e a outra em z = + 1 2 l . Mostre que a magnitude
Um único anel condutor tem raio igual a 3,0c m e conduz corrente igual a 2,6A . Qual é a magnitude do campo magnético na linha que passa pelo centro do anel e é perpendicular ao plano do anel a No cen