UFJF – Física 3 – AV3 – 2ª CH – 2016.2 – Questão 2b
Uma bobina de espiras foi enrolada num corpo toroidal de raio interno , raio externo e altura , como indica a figura ao lado.
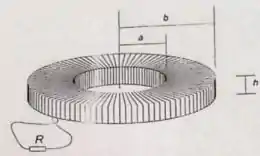
- Calcule a autoindutância desta bobina usando o resultado do item a).
Passo 1
Eaee!!! Belezinha? Bom... a questão nos dá uma bobina em formato toroidal e nos pede para calcular a autoindutância dela usando o resultado do campo magnético que descobrimos no item a), ou seja:
Onde é o campo magnético, é a permeabilidade magnética, é o número de espiras, e é um alor que varia de até .
Lembrando que a autoindutância pode ser calculada da seguinte forma:
Onde é o fluxo magnético.
E aí? Bora responder?
Passo 2
Bom... Para calcular a autoindutância, determinaremos primeiro o fluxo magnético, o qual é dado por:
Sendo o elemento de área da seção transversal do toroide, dado por:
Assim, temos que o fluxo é dado por:
Passo 3
Assim, podemos substituindo o valor de , temos:
Passo 4
Por fim, substituindo o valor do fluxo na equação da autoindutância, temos:
Entendeu direitinho? Responde aee ;)
