UFJF – Física 3 – AV3 – 2ª CH – 2016.2 – Questão 2a
Uma bobina de espiras foi enrolada num corpo toroidal de raio interno , raio externo e altura , como indica a figura ao lado.
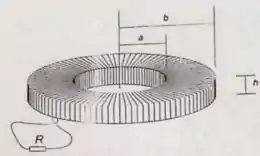
- Escreva o campo magnético gerado por esta bobina quando flui uma corrente no fio enrolado.
Passo 1
Eaee!!! Belezinha? Bom... a questão nos dá uma bobina em formato toroidal e nos pede para dizer o campo magnético quando uma corrente passa pela bobina.
Quando se fala em corrente elétrica e campo magnético, já lembramos da Lei de Ampère!! A qual é dada por:
Onde é o campo magnético, é o diferencial de comprimento, é a permeabilidade magnética e é a corrente envolvida pela amperiana.
E aí? Bora responder?
Passo 2
Bom... Por definição sabe-se que o campo magnético no interior de um toroide o circunda.
Assim, é possível desenhar uma amperiana circular no interior do toroide.
Dessa forma, é constante em toda a amperiana e a integral resulta em , onde varia do ponto até o ponto .
Ademais, a corrente envolvida é igual ao produto do número de espiras pela corrente do sistema.
Passo 3
Assim, substituindo na Lei de Ampère, temos que o campo magnético pode ser descrito como:
Entendeu direitinho? Responde aee ;)
