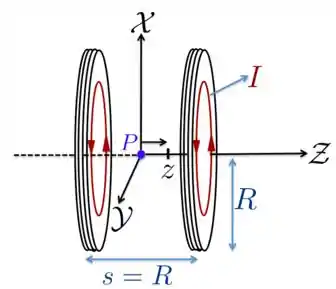
A figura abaixo mostra a seção reta de duas bobinas circulares com raio , cada uma delas com espiras que conduzem uma corrente no mesmo sentido. A distância entre as bobinas é igual ao raio das bobinas. As bobinas dessa configuração denominam-se bobinas de Helmholtz e produzem um campo magnético bastante uniforme na região entre elas. O ponto está à mesma distância do centro de cada uma das duas bobinas.
- Deduza uma expressão para o módulo do campo magnétido em um ponto situado a uma distância à direita do ponto , que está no centro de simetria das bobinas.
- Usando a expressão obtida no item a), obtenha o módulo do campo magnético exatamente sobre o ponto .
- Calcule o valor do módulo do campo magnético no ponto , considerando espiras, e .
Passo 1
A gente viu várias vezes aqui durante os exercícios de fixação, que o módulo campo magnético produzido por uma bobina compacta no ponto sobre o eixo de simetria, abaixo ou acima do plano da bobina, pode ser calculado como vezes o campo produzido em por uma única espira, ou seja,
Note que, independente de o ponto estar à esquerda ou direita do plano da bobina, o campo magnético no ponto aponta na direção e sentido de , pois tomamos o sentido da corrente como está indicado na figura. Tranquilo? Dá uma checada nisso, porque isso é muito importante para a gente resolver este exercício aqui!! Guarda no coração isso...\0/
Passo 2
a) Bom, pra gente obter uma expressão para o campo no ponto a uma distância à direita do ponto da figura, precisamos notar que, a espira da esquerda produz um campo magnético no ponto que é dado por
e a espira da direita produz um campo magnético em dado por
Portanto, como os dois campos acima apontam na mesma direção e sentido dado por , o campo resultante no ponto à direita de é tem a seguinte expressão:
Essa é a expressão geral para o módulo do campo magnético em qualquer ponto sobre o eixo que passa pelo centro das duas bobinas!
CUIDAAAADOOOOOO: tá escrito aí que: “CAMPO MAGNÉTICO EM QUALQUER PONTO SOBRE O EIXO QUE PASSA PELO CENTRO DAS DUAS ESPIRAS SEPARADAS POR ”
Fica de olho nisso...
Passo 3
b) Para gente saber como é o campo no ponto , basta fazer na expressão acima para , o que nos dá o seguinte:
Se simplificamos essa expressão, obtemos que
Passo 4
c) Com os valores dados no enunciado, encontramos que o campo no ponto tem o seguinte valor