Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Campo Magnético Gerado por uma Bobina

Ver Teoria
Exercício 71234568910111213141516171819202122232425262728293031323334353637383940

Enunciado

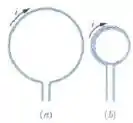
A figura a abaixo mostra um fio que conduz uma corrente i e forma uma bobina circular com apenas uma espira. Na figura b um fio de mesmo comprimento forma uma bobina circular com duas espiras de raio igual à metade do raio da espira da figura a .

( a ) Se B a e B b são os módulos dos campos magnéticos nos centros das duas bobinas, qual é o valor da razão B b / B a ?

( b ) Qual é o valor da razão μ a / μ b entre os momentos dipolares das duas bobinas?

Passo 1

Vamos lá, galera! Nesse exercício, temos uma bobina circular com uma espira que conduz uma corrente i e que tem um raio que chamaremos de R a .

Temos também uma segunda bobina, só que essa é formada por duas espiras de raio R b = R a 2 .

Primeiramente, queremos saber a razão entre os campos no centro das bobinas, B b / B a .

Passo 2

( a )

Sabemos que o módulo do campo magnético a uma distância z do centro de uma bobina de N espiras é dado por:

B z = N μ 0 i R 2 2 R 2 + z 2 3 2

Logo, quando z = 0 , temos:

B z = N μ 0 i 2 R

Assim:

B b B a = 2 μ 0 i 2 R b . 2 R a μ 0 i = 2 R a R b = 4

Passo 3

( b )

O momento dipolar magnético de uma bobina é dado por:

μ = N i A

Assim,

μ a μ b =   i A a 2 . i A b = π 2 R b 2 2 π R b 2 = 2 2 . 1 2 = 2

Resposta

a   4

b   2

Exercícios de Livros Relacionados

79- Uma bobina de alto-falante. Na seção 27.7 , mostramos que era igual a zero a força resultante sobre uma espira de corrente em um campo magnético uniforme. A força magnética sobre uma bobina destin
87- Uso da Lei de Gauss do magnetismo. Em uma certa região do espaço, o campo magnético B → não é uniforme. O campo magnético possui um componente z e outro componente que aponta para fora ou para den
Um solenóide de comprimento 30 cm, raio 1,2 cm e 300 voltas, conduz corrente de 2,6 A. Determine a magnitude do campo magnético no eixo do solenóide:a) No centro do solenóide.b) Em uma extremidade do
Um solenóide tem n voltas por unidade de comprimento, raio R e conduz uma corrente I. Seu eixo coincide com o eixo z – uma extremidade em z = - 1 2 l e a outra em z = + 1 2 l . Mostre que a magnitude
Um único anel condutor tem raio igual a 3,0c m e conduz corrente igual a 2,6A . Qual é a magnitude do campo magnético na linha que passa pelo centro do anel e é perpendicular ao plano do anel a No cen