A figura abaixo mostra uma Bobina de Helmholtz, um dispositivo utilizado para produzir uma região de campo magnético razoavelmente uniforme. Este dispositivo também é usado em aparatos de pesquisa para cancelar o campo magnético da Terra (entre diversas outras aplicações).
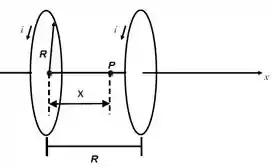
O dispositivo consiste de duas espiras circulares de raio , ambas perpendiculares ao eixo de simetria, com seus centros separados por uma distância também igual a . As duas carregam correntes fluindo no mesmo sentido.
- Calcule o campo magnético sobre o eixo, devido à espira da esquerda, no ponto situado a uma distância (medida a partir do centro desta espira) entre as duas espiras (módulo, direção, sentido). ATENÇÃO: o ponto NÃO está situado no centro das espiras, mas em uma posição genérica do eixo entre as espiras.
- Calcule o campo magnético no mesmo ponto devido à outra espira (módulo, direção, sentido).
- Qual é o campo magnético total em (módulo, direção, sentido)?
- A partícula será defletida ou continuará na sua direção e sentido? Se mantiver direção e sentido, justifique. Se não, descreva qualitativamente em que direção e sentido a partícula será defletida.
Considere agora uma partícula carregada, , com carga negativa, que passa no ponto (onde o campo magnético é praticamente uniforme) com uma velocidade , onde é uma constante.
Passo 1
Para calcular o campo vamos usar a lei de Biot-Savart
Temos que é o vetor cujo comprimento é o infinitésimo de arco e é tangente à curva onde passa a corrente.
Como todos os pontos da espira são equivalentes vamos olhar o vetor posicionado no topo do círculo onde ele estará apontando na direção para facilitar a visualização.
Já o vetor é o unitário que aponta da direção de onde tem corrente até o ponto onde queremos calcular o campo magnético.
Como o infinitésimo do campo magnético é proporcional ao produto vetorial de e , esse campo magnético infinitesimal é perpendicular a esses dois vetores, conforme a figura abaixo
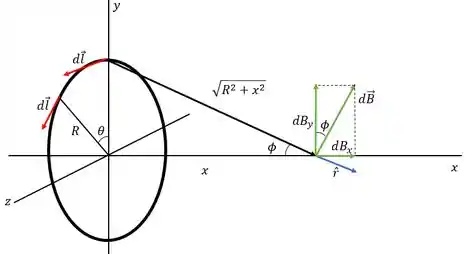
Mas até agora só falamos dos infinitésimos de campo. Quando somarmos todas as contribuições dos pedaços da espira, teremos contribuições que são radialmente opostas. Essas contribuições radialmente opostas terão componentes na direção que se anulam, fazendo com que o nosso campo magnético no final aponte na direção .
Pela regra da mão direita, vemos que o campo magnético tem que apontar na direção indicada na figura e, portanto, a sua componente apontará na direção e no sentido positivo.
Assim não precisamos nos preocupar com a componente do campo! Pela figura vemos que a componente do campo se relaciona com o campo total por
Já a distância é a distância do infinitésimo de corrente até o ponto em que queremos calcular o campo magnético e de acordo com a figura e usando o teorema de Pitágoras
E o seno do ângulo é dado por
Agora voltando com a lei de Biot-Savart, podemos substituir tudo
Agora podemos integrar em (somar todas as contribuições ao longo do círculo)
De forma que o vetor é dado por
Vemos que aponta na direção no sentido positivo.
Passo 2
A segunda espira está uma distância do ponto . Como ela é idêntica a primeira o campo que ela produz será praticamente igual só mudando
Esse campo também apontará na direção , mas qual o sentido? De novo usamos a regra da mão direita!
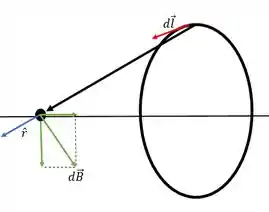
Nesse caso a componente do campo magnético apontará também na direção positiva do eixo ! Assim
Passo 3
O campo total será a soma dos dois campos!
Que aponta na direção positiva do eixo .
Passo 4
Segundo o enunciado podemos considerar o campo praticamente uniforme.
Uma partícula com velocidade passa em uma região com o campo na direção (). Dessa forma a força sobre essa partícula é dada por
Como a carga é negativa podemos rescrever como
Ou seja, quando a partícula passar entre as duas bobinas a força sobre ela será na direção e então ela será defletida nessa direção.
Resposta
(a)
(b)
(c)
(d) Será defletida na direção .