Esta questão é constituída de duas partes independentes.
Parte 1
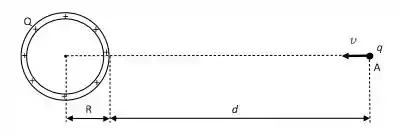
Uma casca esférica isolante de raio possui uma carga positiva uniformemente distribuída. Uma carga negativa e de massa passa pelo ponto A, a uma distância da superfície da casca, com velocidade em direção ao centro da casca esférica, como indicado na figura abaixo. A carga pode ser considerada tão pequena que não influencia a distribuição de cargas na casca esférica.
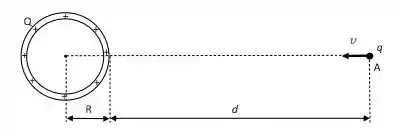
Nesta situação:
a) Calcule o potencial do ponto A.
b) Calcule a velocidade com a qual a carga irá colidir com a casca esférica.
Parte 2
Um sistema de placas planas e paralelas possui um diagrama de potencial de acordo com a figura abaixo.
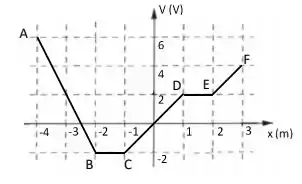
c) Faça o gráfico do valor do campo elétrico indicando claramente os valores do campo em cada região.
d) Na região entre os pontos D e E, a placa é isolante ou condutora? Justifique claramente a sua resposta.
e) Calcule a densidade superficial de carga na superfície B. (para os cálculos, considere )
Passo 1
PARTE 1:
POW! Queremos calcular o potencial feito pela esfera no ponto ...
De acordo com a teoria, uma esfera de carga produz um potencial fora dela que é idêntico ao potencial de uma carga pontual centra no centro da esfera...
Onde é a distância do ponto que estamos buscando o potencial ao centro da origem. No nosso caso...
Só que , então o potencial no ponto será...
Passo 2
Bem, para esse exercício, iremos usar a conservação da energia para encontrar a velocidade que a partícula irá colidir com a esfera.
Sabemos que a variação da energia potencial elétrica é igual à variação da energia cinética ...
Passo 3
A variação da energia potencial elétrica por sua vez depende apenas da variação potencial onde a carga se encontra até onde a carga vai estar...
é o potencial na superfície da esfera que é onde a carga vai estar na colisão. Já é o potencial da carga no ponto (calculado no item anterior).
O potencial na esfera é basicamente a mesma coisa, mas ao invés de teremos apenas (distância de um ponto qualquer da esfera até a origem da esfera)...
Passo 4
Por outro lado, a variação da energia cinética é a energia cinética no ponto final...
Menos a energia cinética inicial (energia cinética no ponto )...
Ou seja...
Veja que é a velocidade final quem estamos buscando, ou seja, ...
Então...
Isolando ...
Passo 5
Bem, sabemos que o campo elétrico (ou pelo menos a componente dele) e o potencial estão associados pela fórmula...
Então o que vamos fazer aqui é pegar o gráfico...
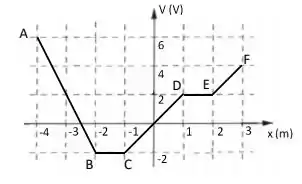
Encontrar a equação dessas retas e depois derivar em cada trecho .
Passo 6
Mas para ser mais rápido ainda, vamos veja bem... Toda reta pode ser escrita como...
Logo...
Então o que temos que encontrar é o coeficiente de cada reta.
O coeficiente pode ser simplesmente ser determinado pegando...
Então veja bem... Para a primeira reta, de a ...
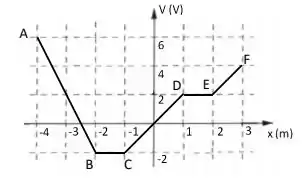
O e o , então...
Ou seja, o campo elétrico para esse primeiro trecho é...
Para o segundo trecho, de a , como temos uma reta constante...
Para o terceiro trecho e ...
No quarto trecho, de a , o potencial volta a ficar constante, o que significa que...
No último trecho, de a , e
Agora é só construir o gráfico inserindo os valores desses potenciais em cada trecho...
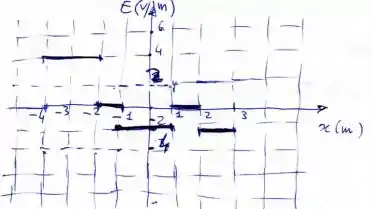
Passo 7
Ora... Sabemos da teoria que o potencial só será constante se o material for um condutor! Assim, como o trecho entre e o potencial é constante, o trecho é um condutor .
Passo 8
Como a placa é um material isolante, na superfície vai haver uma densidade superficial de carga . Só que a placa é um condutor (potencial constante) então o campo elétrico nessa região será . Para isso acontecer, o campo elétrico na placa tem que ser...
Já que da placa o campo é , ta ligado? Assim o total é . A densidade de carga então pode ser relacionada com esse campo elétrico...
Ou seja...
Resposta
Letra A:
Letra B:
Letra C:
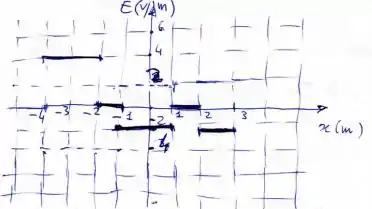
Letra D: Condutor.
Letra E: