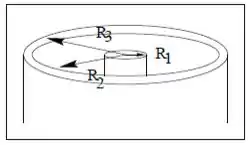
Considere o sistema, mostrado em corte na figura ao lado, que é constituído por uma casca cilíndrica fina de raio e comprimento infinito na qual flui uma corrente para cima e, coaxial a ela, uma outra casca cilíndrica, desta vez com raio interno e externo e também comprimento infinito, com uma corrente () apontando para baixo.
Calcule o vetor campo magnético em todas as regiões sabendo que as correntes estão distribuídas uniformemente.
Passo 1
Olá, tudo tranquilo? Vamos resolver essa questão de magnetismo? O problema nos dá um sistema que tem um fio com corrente apontando para cima e uma casca cilíndrica (por fora desse fio) com raio e , que percorre uma corrente para baixo
Saca só o esboço desse sistema
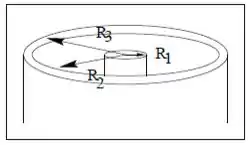
Para determinar o campo magnético em todas as regiões, vamos usar a lei de Ampère, ela diz o seguinte:
Nossa curva será um círculo, pela simetria, temos que o campo magnético (dado pela regra da mão direita), será sempre paralelo ao vetor , e será sempre constante, temos então:
Então a ideia é em cada região
Aplicar a Lei de Ampére, levando em conta a magnitude das correntes () e o sentido delas!

Mas pode ficar tranquilo, vou fazer passo a passo com você!
 Vamos começar?
Vamos começar?
Passo 2
Vamos começar pela primeira região:
Para essa região, a corrente interna vai variar para cada valor de , por isso precisamos determinar a corrente para cada valor de ! A corrente por unidade de área é dada por:
Para diferentes valores de , a corrente fica:
Agora é só jogar na lei de Ampère!
Tranquilo?

Passo 3
Agora fazendo para a segunda região:
Para essa região, temos que a corrente interna será toda a corrente que passa no cilindro central (), a Lei de Ampère fica assim:

Passo 4
Agora nossa missão é achar o campo na região . Lembrando que flui pra cima e fui pra baixo!

Para essa região, devemos fazer o mesmo raciocínio da região , pois a corrente interna na casca vai variar com , temos então que a corrente por unidade de área é dada por:
Para diferentes valores de , a corrente interna fica:
Vamos agora aplicar a Lei de Ampère, mas lembre-se, não podemos esquecer da corrente que passa pelo cilindro central, a corrente interna à Amperiana será:
Beleza?

Agora sim, vamos aplicar a Lei de Ampère:
Tranquilo? Estamos quase no final!
Passo 5
Nossa última região é em , nessa região vamos somar (levando em conta o sentido delas) as correntes, pois elas estarão completas dentro da nossa amperiana!
E o campo magnético nesse ponto é
E é isso! Espero ter ajudado!
#partiu treinar mais?