Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Campo Magnético Gerado por uma Bobina

Ver Teoria
Exercício 40123456789101112131415161718192021222324252627282930313233343536373839

Enunciado

Considere uma esfera isolante de raio R com uma carga total q distribuída de maneira esfericamente simétrica seguindo a densidade volumétrica de carga ρ r =   ρ 0 r n R n onde   r é a distância ao centro da esfera (Figura 1).

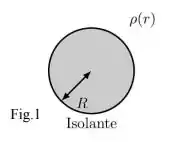
a) Encontre o campo elétrico E → na região externa à esfera ( r   >   R ) .

b) Encontre o valor de n para que o campo elétrico no interior da esfera cresça com o quadrado da distância r ; isto é, como E ( r )   =   β r 2 . Para esse valor de n , encontre β .

Em seguida, a esfera é envolvida por uma casca esférica condutora de raio interno 2 R e raio externo   3 R , como mostra a Figura 2. Essa casca possui uma carga líquida Q desconhecida.

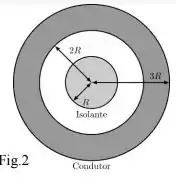
c) Encontre a densidade superficial de carga σ i na parede interna da casca condutora (raio 2 R ).

d) Se o módulo do campo elétrico a uma distância r   =   4 R for   E ( 4 R )   = q / 128 π ε 0 R 2 , qual é o valor da carga líquida Q ?

Passo 1

Nesse exercício, podemos encontrar o campo elétrico de diversas maneiras. Mas acredito que a forma mais simples que a forma mais simples que você poderá pensar na sua provinha é resolver usando a Lei de Gauss...

∯ G   E →   d A → = Q i n t ε 0

Onde G é a Gaussiana, uma superfície fechada que a gente escolhe na região onde queremos buscar o campo elétrico E → . Q i n t é a carga elétrica dentro da Gaussiana.

Passo 2

L e t r a   A :

POW! Na região externa a esfera, podemos escolher uma Gaussiana esférica tal que o raio da Gaussiana r seja maior que o raio da esfera R ...

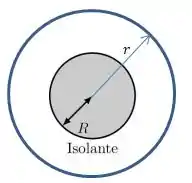
Repare que o campo elétrico da esfera carregada é sempre radial, isto é, sempre perpendicular a superfície da Gaussiana...

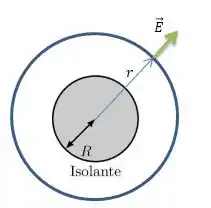
E olha que maneiro cara, o campo elétrico é perpendicular à superfície da esfera (Gaussiana), o que é o mesmo que dizer que o campo elétrico então tem a mesma direção que o vetor de área da superfície da Gaussiana...

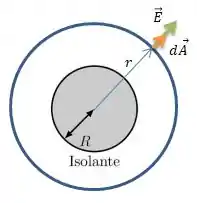
Pela álgebra, se tivermos dois vetores na mesma direção o produto vetorial deles será apenas o produto dos módulos (tamanhos). Sendo assim, podemos dizer que o produto escalar entre os vetores E → ⋅ d A → é igual ao produto dos módulos, isto é...

E → ⋅ d A → = E   d A

Então...

∯ G   E →   d A → = Q i n t ε 0     →     e q u a ç ã o   1

∯ G   E   d A = Q i n t ε 0     →

Como o campo elétrico é constante ao longo de toda a Gaussiana...

E ∬ G     d A = Q i n t ε 0     →

E agora quem é a integral de d A ? Isso mesmo! É a área da Gaussiana!

E   4 π r 2 = Q i n t ε 0     →

E   = Q i n t 4 π ε 0 r 2    

Só que o problema nos disse que a esfera tem carga q , então a carga dentro da Gaussiana é justamente essa carga q ...

E   = q 4 π ε 0 r 2    

Ou em termos de vetor, o campo elétrico é radial, isto é na direção r ^ , então...

E → = q 4 π ε 0 r 2   r ^

Passo 3

L e t r a   B :

Para esse problema de agora, vamos fazer algo semelhante, isto é, vamos traçar uma Gaussiana e usar a Lei de Gauss para descobrirmos o valor do campo elétrico, mas dessa vez dentro da esfera de carga, isto é r < R ...

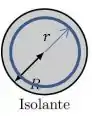
Aplicando então a Lei de Gauss novamente, vamos encontrar...

E   = Q i n t 4 π ε 0 r 2    

Só que agora tem um porém... A carga interna Q i n t que está dentro da Gaussiana não será mais q , já que estamos falando de uma Gaussiana no interior do cilindro de carga. Mas então quem será Q i n t ?

Passo 4

Podemos falar que a carga interna da Gaussiana é a integral de volume da densidade de carga, isto é...

Q i n t = ∭ I G     ρ r   d V

Onde I G significa Interior da Gaussiana.

Ora... O interior da Gaussiana, é uma esfera, então nem precisa calcular essa integral tripla, pois eu vou te dar um bizu, anota aí!

Toda vez que você tiver que calcular uma integral tripla dentro de uma esfera, onde função de integração só depende do raio, então você pode fazer usar a fórmula...

Q i n t = ∫ r 1 r 2   4 π r 2 ρ r   d r

Onde r 1 é o raio inicial e r 2 o raio final. No nosso caso, r 1 = 0 e r 2 = R . Substituindo ρ r também...

Q i n t = ∫ r 1 r 2   4 π r 2 ρ 0 r n R n   d r     →

Integrando...

Q i n t = 4 π ρ 0 R n   ∫ r 1 r 2   r n + 2   d r     →

Q i n t = 4 π ρ 0 R n   r n + 3 n + 3 r 1 r 2     →

Substituindo...

Q i n t = 4 π ρ 0 R n   r 2 n + 3 n + 3 - r 1 n + 3 n + 3     →

Como o raio inicial é 0 e o raio final é a o raio da Gaussiana ( r 2 = r ), dessa forma toda a esfera ficará descrita, então...

Q i n t = 4 π ρ 0 R n   r n + 3 n + 3  

Passo 5

Com a carga interna encontrada, podemos substituir na equação onde paramos no passo 3...

E   = Q i n t 4 π ε 0 r 2 →

E   = 1 4 π ε 0 r 2 ⋅ 4 π ρ 0 R n   r n + 3 n + 3       →

Simplificando, o campo elétrico no interior da esfera será...

E   = 1 ε 0 r 2 ⋅ ρ 0 R n   r n r 3 n + 3       →

E   = r ρ 0 n + 3 ε 0   r n R n    

O problema nos pediu para encontrar o valor de n tal que o campo elétrico fosse E ( r )   =   β r 2 , no interior da esfera...

β r 2 = r ρ 0 n + 3 ε 0   r n R n     →

Reorganizando esse lado direito de modo a ficar algo parecido com o lado esquerdo...

β r 2 = ρ 0 n + 3 ε 0 R n   r n + 1     →

Então...

n + 1 = 2     →

n = 1

E veja que também conseguimos tirar daí o valor de β ...

β = ρ 0 n + 3 ε 0 R n     →

β = ρ 0 1 + 3 ε 0 R 1 = ρ 0 4 ε 0 R

Passo 6

L e t r a   C :

Ora, a carga elétrica da esfera de dentro é q ...

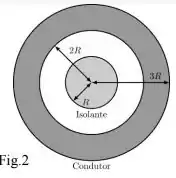
Então a carga elétrica atraída na superfície interna da esfera condutora tem que ser - q . Portanto, a densidade de carga na superfície interna da esfera condutora será...

σ i = - q A r e a

Onde A r e a é a área da superfície interna da esfera condutora. Como a superfície interna é uma esfera de raio 2 R , a área será...

A r e a = 4 π 2 R 2     →

A r e a = 4 π 4 R 2   →

A r e a = 16 π R 2

Então...

σ i = - q 16 π R 2

Passo 7

L e t r a   D :

Pela Lei de Gauss para uma Gaussiana de r = 4 R ...

E   = Q i n t 4 π ε 0 4 R 2 →

E   = Q i n t 64 π ε 0 R 2

Só que o problema nos disse que o campo elétrico a uma distância de 4 R vale...

E ( 4 R )   = q 128 π ε 0 R 2

Então...

Q i n t 64 π ε 0 R 2 = q 128 π ε 0 R 2     →

Q i n t = q 2

Só que a carga interna que está sendo envolvida pela Gaussiana a uma distância de 4 R é a carga do isolante ( q ) e a carga da esfera condutora Q , então...

Q + q = q 2

E, portanto...

Q = - q 2

Resposta

Letra A:

E → = q 4 π ε 0 r 2   r ^

Letra B:

n = 1             e               β = ρ 0 4 ε 0 R

Letra C:

σ i = - q 16 π R 2

Letra D:

Q = - q 2

Exercícios de Livros Relacionados

79- Uma bobina de alto-falante. Na seção 27.7 , mostramos que era igual a zero a força resultante sobre uma espira de corrente em um campo magnético uniforme. A força magnética sobre uma bobina destin
87- Uso da Lei de Gauss do magnetismo. Em uma certa região do espaço, o campo magnético B → não é uniforme. O campo magnético possui um componente z e outro componente que aponta para fora ou para den
Um solenóide de comprimento 30 cm, raio 1,2 cm e 300 voltas, conduz corrente de 2,6 A. Determine a magnitude do campo magnético no eixo do solenóide:a) No centro do solenóide.b) Em uma extremidade do
Um solenóide tem n voltas por unidade de comprimento, raio R e conduz uma corrente I. Seu eixo coincide com o eixo z – uma extremidade em z = - 1 2 l e a outra em z = + 1 2 l . Mostre que a magnitude
Um único anel condutor tem raio igual a 3,0c m e conduz corrente igual a 2,6A . Qual é a magnitude do campo magnético na linha que passa pelo centro do anel e é perpendicular ao plano do anel a No cen