Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Campo Magnético Gerado por uma Bobina

Ver Teoria
Exercício 19123456789101112131415161718202122232425262728293031323334353637383940

Enunciado

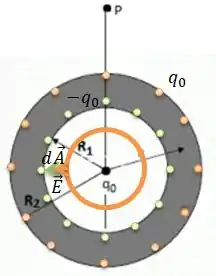
Uma carga pontual positiva, q 0 , dada em C está situada no centro de uma casca esférica condutora, em equilíbrio eletrostático e eletricamente neutra, de raio interno R 1 e raio externo R 2 , ( R 1 < R 2 ), medidos em m (veja figura abaixo).

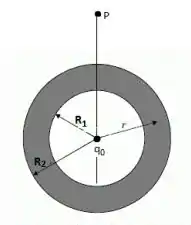
  1. Quais as cargas induzidas, respectivamente, na superfície interna e na superfície externa da casca?
  2. Seja r a distância radial ao centro da casca esférica medida em m . Calcule o vetor campo elétrico em todas as regiões do espaço, i.e., para r   <   R 1 , para R 1 < r < R 2 , e para r > R 2 .

Passo 1

L e t r a   A :

Cara... Pensa comigo... Tínhamos ali a esfera eletricamente neutra e condutora. Imediatamente após inserir a carga positiva q 0 no seu interior, o que vai acontecer?

Ora... As cargas livres na esfera vão se locomover de modo que na superfície interna surja uma carga de mesmo módulo q 0 mas de sinal contrário a carga do interior, ou seja, - q 0 ...

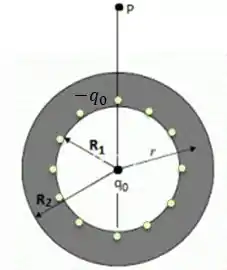
E na casca mais exterior da esfera vão estar às cargas positivas espalhadas uniformemente de modo que todas juntas formam q 0 !

Passo 2

L e t r a   B :

Para encontrar o campo elétrico em todas as regiões, vamos utilizar a Lei de Gauss que nos fala que...

∯ G   E → ⋅ d A → = q i n t ε 0

Onde G é a Gaussiana (uma superfície fechada que a gente escolhe na região onde estamos buscando o campo elétrico), q i n t é a carga interna dentro da Gaussiana escolhida.

Dessa forma, por exemplo, se quisermos calcular o campo elétrico na região de dentro r < R 1 , a gente escolhe uma Gaussiana esférica de raio r ...

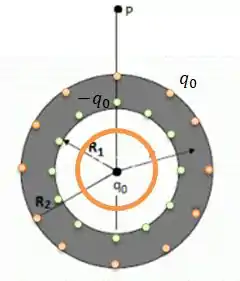
Repare que a carga interna dentro dessa Gaussiana é q i n t = q 0 , então, pela Lei de Gauss...

∯ G   E → ⋅ d A → = q 0 ε 0

Agora, qual é a solução dessa integral de superfície?

Passo 3

Cara... O campo elétrico de uma carga pontual é sempre radial (direção r ^ ) de modo que ele terá sempre a mesma direção que o vetor d A → (vetor de área da Gaussiana)...

E de acordo com a nossa Álgebra, o produto vetorial de dois vetores que possuem a mesma direção, será igual ao produto dos módulos...

E → ⋅ d A → = E   d A

Então...

∯ G   E → ⋅ d A → = q 0 ε 0     →

∯ G   E   d A = q 0 ε 0

Como o campo elétrico é constante ao longo de uma esfera de raio r da carga q 0 ...

E ∯ G   d A = q 0 ε 0

Ora... A integral de d A é conhecida por ser igual à área da superfície G . Como a nossa superfície é uma esfera de raio r ...

E 4 π r 2 = q 0 ε 0     →

E = q 0 4 π ε 0 r 2  

Então, o vetor campo elétrico para r < R 1 será...

E → = q 0 4 π ε 0 r 2   r ^

Passo 4

Agora vamos calcular o campo elétrico para a região dentro do condutor e para isso, vamos escolher uma Gaussiana agora que tenha raio r , onde R 1 < r < R 2 ...

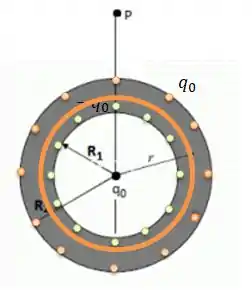
De acordo com a Lei de Gauss...

∯ G   E → ⋅ d A → = q i n t ε 0

Só que repare que a carga interna na Gaussiana dessa vez é q i n t = q 0 - q 0 = 0 ...

∯ G   E → ⋅ d A → = 0

Então o campo elétrico nessa região é 0 .

E = 0

Passo 5

Por último, vamos calcular o campo elétrico fora de tudo, ou seja, R 2 < r ...

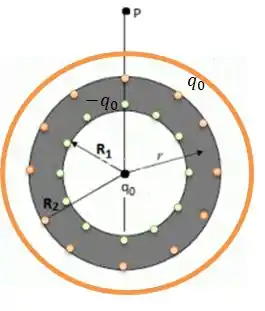
Repare que aí a carga interna na Gaussiana vai ser q i n t = q 0 - q 0 + q 0 = q 0 ...

∯ G   E → ⋅ d A → = q 0 ε 0

Então, de modo semelhante ao passo 3...

E 4 π r 2 = q 0 ε 0   →

E = q 0 4 π ε 0 r 2

Então, o vetor campo elétrico para R 2 < r também será...

E → = q 0 4 π ε 0 r 2   r ^  

Resposta

Letra A:

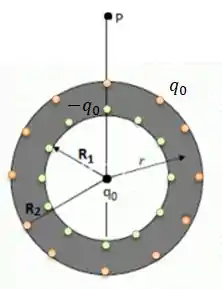
Letra B:

r < R 1       →               E → = q 0 4 π ε 0 r 2   r ^

R 1 < r < R 2       →               E → = 0

R 2 < r             →             E → = q 0 4 π ε 0 r 2   r ^

Exercícios de Livros Relacionados

79- Uma bobina de alto-falante. Na seção 27.7 , mostramos que era igual a zero a força resultante sobre uma espira de corrente em um campo magnético uniforme. A força magnética sobre uma bobina destin
87- Uso da Lei de Gauss do magnetismo. Em uma certa região do espaço, o campo magnético B → não é uniforme. O campo magnético possui um componente z e outro componente que aponta para fora ou para den
Um solenóide de comprimento 30 cm, raio 1,2 cm e 300 voltas, conduz corrente de 2,6 A. Determine a magnitude do campo magnético no eixo do solenóide:a) No centro do solenóide.b) Em uma extremidade do
Um solenóide tem n voltas por unidade de comprimento, raio R e conduz uma corrente I. Seu eixo coincide com o eixo z – uma extremidade em z = - 1 2 l e a outra em z = + 1 2 l . Mostre que a magnitude
Um único anel condutor tem raio igual a 3,0c m e conduz corrente igual a 2,6A . Qual é a magnitude do campo magnético na linha que passa pelo centro do anel e é perpendicular ao plano do anel a No cen