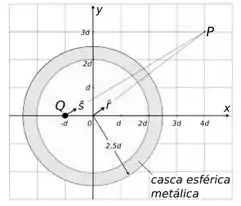
7 - Uma carga pontual Q é posicionada dentro de uma casca esférica metálica neutra, conforme indicado na figura. O vetor campo elétrico no ponto P é dado por:
Passo 1
Bem! Sabemos que um ponto carregado dentro de uma esfera oca faz com que cargas livres dentro da esfera se organizem nas superfícies da esfera da seguinte maneira (para entender, vamos supor que a carga seja positiva):
- Essa carga atrai carga negativa na superfície interna:
- Essas cargas negativas repelem cargas positivas na superfície externa:
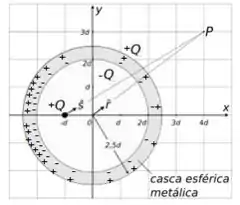
Claro, no nosso caso vai haver uma concentração de cargas maior perto do ponto carregado interno como a gente pode ver.
O campo que enxergará então será o campo da carga no exterior de mesmo sinal e valor da carga puntiforme: . Mas qual é o valor desse campo?
Passo 2
Ora, pela teoria, o campo observado de uma e esfera carregada é o mesmo campo de uma partícula no centro da esfera:
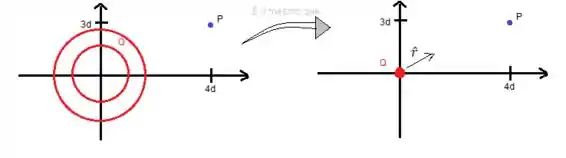
E isso é válido independente da distribuição de cargas na superfície dela, saca? Eu sei! Às vezes somos levados a pensar que não, mas nesse caso sim .
O módulo campo elétrico de um ponto carregado é:
Como a gente deve considerar essa esfera no centro, o vetor campo elétrico no ponto vai ter o sentido de :
Agora só falta descobrir quem é esse !
Passo 3
Esse indica a distância do ponto até a carga. Como a esfera pode ser considerada uma carga puntiforme no centro, temos que encontrar a distância de até o centro (origem do cartesiano).
Ora, o ponto está no ponto , então a distância do a origem será por Pitágoras:
Então o nosso campo elétrico será...
Resposta
Letra B.