O campo elétrico produzido por uma distribuição esfericamente simétrica de cargas tem a forma , onde é a distância até a origem de um sistema de coordenadas, que coincide com o centro da distribuição, e  é o vetor unitário da direção radial. O gráfico é mostrado na figura abaixo. Considere que a distribuição se encontra em equilíbrio eletrostático, que e que .

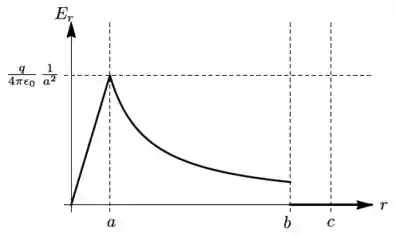
Sobre essa distribuição, considere as seguintes afirmativas abaixo:

1. A região está preenchida por um material isolante uniformemente carregado.
2. A região está preenchida por um material condutor perfeito.
3. A carga total contida na região é nula.

São VERDADEIRAS as seguintes afirmativas:

3. e
5. e
6. e
7. , e
8. Nenhuma delas.

Vamos começar analisando a afirmação . Se o material que está nessa região é preenchido por um isolante cuja carga está uniformemente distribuída, então se fizermos uma gaussiana esférica com raio , como está na figura abaixo, a carga que está dentro dessa gaussiana é

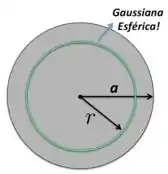
Como temos simetria esférica, então o campo elétrico produzido pela carga positiva terá o mesmo valor sobre todos os pontos da gaussiana e será paralelo ao vetor elemento de área  em todos os pontos dessa superfície.

Por isso, a lei de Gauss vai dar o seguinte:

Quando simplificamos essa expressão, vamos obter que o módulo do campo produzido pela carga positiva dentro de será igual a

que cresce linearmente com a distância ao centro da esfera. Portanto, a afirmativa está correta: um isolante uniformemente carregado produz um campo elétrico linear com na região .