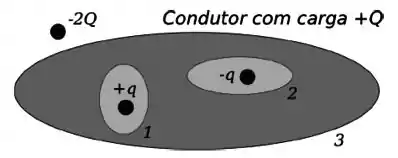
Considere um material condutor com carga positiva com duas cavidades em seu interior, conforme figura. Na cavidade 1 existe uma carga positiva . Na cavidade 2 existe uma carga negativa . Fora do condutor, temos ainda uma carga negativa . A carga total no condutor está distribuída de acordo com:

1. na superfície 1; na superfície 2; na superfície 3.
2. na superfície 1; na superfície 2; na superfície 3.
3. na superfície 1; na superfície 2; na superfície 3.
4. na superfície 1; na superfície 2; na superfície 3.
5. nas três superfícies.

Vamos começar analisando a cavidade 1. Como tem uma carga positiva dentro dessa região, ela vai induzir uma carga negativa sobre a superfície interna da cavidade 1, como mostra a figura abaixo. Na superfície interna da cavidade 2, haverá uma carga induzida positiva .

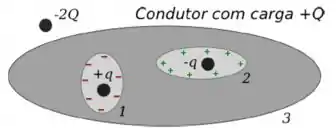
Se a presença da carga induz uma carga na superfície interna da cavidade 1, então sobre a superfície 3 haverá uma carga adicional induzida de valor . Da mesma maneira, por causa da carga , haverá uma carga induzida na superfície 3. Portanto, na superfície 3 do condutor, teremos uma carga total de

Repara que se as cargas dentro das regiões 1 e 2 fossem, respectivamente, e , então, no equilíbrio eletrostático, a carga total que estaria sobre a superfície 3 seria:

Então, nesse caso, na superfície interna da região 1, haveria uma carga e na superfície interna de 2, uma carga de !!

Fica ligad@ nesse detalhe, beleza??

Conselho? Tenta reproduzir esse problema com as cargas e para fixar as ideias!! ;-)