Física 3 – UNICAMP – 2019.1 – Exame – Questão 1
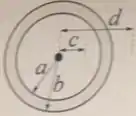
Uma carga puntiforme está no centro de uma camada esférica condutora de raio interno e raio externo . A uma distância da carga, o campo elétrico tem módulo e aponta radialmente para fora. A uma distância da carga, o campo elétrico tem módulo e aponta radialmente para dentro da camada. Determine em função de , , , , , e :
a) O valor e o sinal da carga puntiforme.
b) O sinal e o valor da carga na superfície externa da camada condutora.
Passo 1
Fala galerinha, bora brincar um pouco com condutores e campo elétrico? Partiu!!!
No centro de um condutor esférico de raio interno e raio externo é colocada uma carga pontual . Numa distância , portanto dentro da camada interna do condutor, o campo é e aponta para fora.
A única fonte para esse campo é a carga e, como ele aponta para fora, essa carga deve ser positiva. O campo dessa carga pontual é
Esse foi o item (a).
Passo 2
No item (b) queremos saber a carga acumulada na superfície externa do condutor. Primeiro, vamos achar a carga acumulada na superfície interna!
Sabemos que dentro do condutor o campo elétrico deve ser nulo. Assim, a carga acumulada na superfície interna do condutor deve ser igual a , para anular completamente a carga pontual .
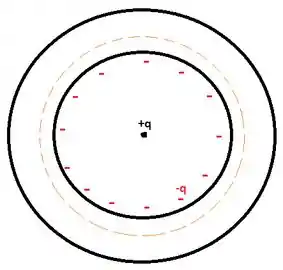
Com isso, a carga envolta pela esfera laranja pontilhada é nula e o campo no interior do condutor é nulo.
Passo 3
Vamos considerar que a carga acumulada na superfície externa do condutor é . Como o resto das cargas se anulam, é apenas essa carga que é responsável pelo campo fora do condutor, para .
Mas nessa situação, o campo aponta para dentro, de modo que deve ser negativo. Assim, temos que
E com isso fechamos o problema 😉!