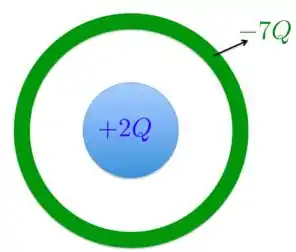
Considere a esfera sólida condutora e a casca esférica condutora concêntrica mostrada na Figura abaixo. A casca esférica tem carga . A esfera sólida tem carga .
- Quanta carga está na superfície interna da casca esférica?
- Considere, agora, que um fio metálico seja conectado entre a esfera sólida e a casca. Depois de o equilíbrio eletrostático ser restabelecido, quanta carga está na esfera sólida e em cada superfície da casca esférica? O campo elétrico na superfície da esfera sólida varia quando o fio é conectado? Se a resposta for positiva, de que maneira?
Passo 1
a) Como a casca esférica externa é condutora, o campo elétrico no interior dela, no equilíbrio eletrostático, é zero. Ou seja, no interior da região verde da Figura, o campo elétrico é zero e qualquer excesso de carga nessa casca vai para a superfície dela.
O mesmo acontece com a esfera sólida que está dentro da casca. A carga dela está uniformemente distribuída sobre sua superfície e não tem campo elétrico dentro dessa esfera sólida.
Bom, como a carga líquida de todo o sistema é , então, uma carga de vai ficar na superfície interna da casca esférica, no equilíbrio eletrostático, como está na Figura abaixo. O restante da carga total da casca esférica, que é , vai para a sua superfície externa.
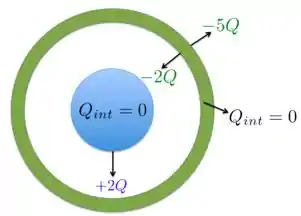
Passo 2
b) Agora, dá uma olhada na Figura acima. Se a gente conectar um fio condutor entre a superfície da esfera condutora sólida e superfície interna da casca condutora, haverá um cancelamento das cargas e após o equilíbrio eletrostático ser restabelecido e restará apenas a carga sobre a superfície externa da casca esférica, que não é alterada.
Nessa situação, não haverá campo elétrico entre as esferas, já que haverá cancelamento das cargas por causa do fio condutor, mas haverá campo elétrico na parte externa à casca esférica, já que esta, independentemente do fio condutor, permanece com carga .
Resposta
- Na região no interior da casca esférica não haverá carga e estará sobre a superfície externa da casca esférica.