Considere o corte plano de um condutor, em equilíbrio eletrostático, com fronteira , conforme mostrado na figura abaixo; a parte sombreada representa o interior do condutor.
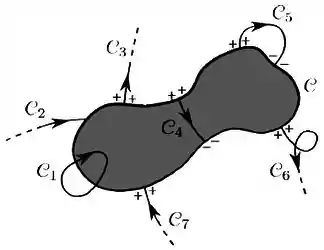
Das curvas , , todas no próprio plano de corte da figura, qual(is), nitidamente, não pode(m) representar linha(s) de campo elétrico?
e .
e .
e .
e .
.
Passo 1
Vamos analisando uma curva por vez.
A curva passa por dentro do condutor, no entanto, não existe campo elétrico no interior de um condutor, logo, não pode representar uma linha de campo.
A curva entra em uma região com carga neutra. Para que o campo elétrico estivesse entrando no condutor, deveriam haver cargas negativas na região. Logo, não pode representar uma linha de campo.
A curva representa o campo saindo de uma região com cargas positivas. Logo, está correto.
A curva passa pelo interior do condutor, onde não há campo elétrico. Logo, não pode representar uma linha de campo.
A curva tem um formato que não é característico das linhas de campo elétrico. Logo, não pode representar uma linha de campo.
A curva está entrando numa região com cargas positivas. Quando, na verdade, as linhas de campo saem das cargas positivas e entram nas cargas negativas. Logo, não pode representar uma linha de campo.
Em relação à curva , ela não pode representar uma linha de corpo porque ela sai e entra no mesmo corpo.
Logo, a única possível é a letra .
Resposta
e .