Um condutor esférico contém, em seu interior, uma cavidade esférica concêntrica. Uma partícula com carga encontra-se no centro da cavidade e o condutor, em equilíbrio eletrostático, possui carga elétrica total . Sendo o campo elétrico resultante em um ponto P fora do sistema, assinale o único item correto.
(a) ≠ e a carga total na superfície externa do condutor é zero.
(b) ≠ e a carga total na superfície externa do condutor é .
(c) = e a carga total na superfície externa do condutor é .
(d) = e a carga total na superfície externa do condutor é .
(e) = e a carga total na superfície externa do condutor é zero.
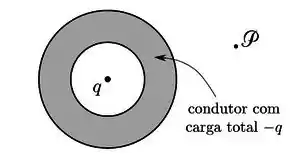
Passo 1
Primeiramente temos que lembrar que dentro de um condutor o campo elétrico é sempre zero.
Se traçarmos uma gaussiana (em laranja) esférica concêntrica dentro do condutor, o campo elétrico deverá ser zero.
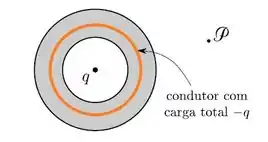
Passo 2
Aplicamos a lei de gauss:
Como temos uma simetria esférica vamos ficar com a expressão: .
Como a gaussiana está localizada no interior de um condutor, o campo elétrico é zero e então:
Mas a carga no interior da nossa gaussiana é dada pela soma da carga da partícula no centro da esfera MAIS as cargas localizadas na superfície esférica interna:
Rearranjando, temos:
Como a carga total da esfera condutora é , toda esta carga estará na superfície interna e nenhuma estará na superfície externa.
Passo 3
Finalmente, se traçarmos uma gaussiana esférica concêntrica passando pelo ponto P e aplicando a lei de gauss novamente, teremos que a carga interna é igual a zero pois:
E, portanto, o campo elétrico será zero também:
Passo 4
Portanto, temos que o campo elétrico no ponto P é igual a zero e não há cargas na superfície externa da esfera.
A alternativa correta é a letra (e).
Resposta
(e) = e a carga total na superfície externa do condutor é zero.