9ª questão - Considere 3 esferas condutoras idênticas de raio . A primeira esfera, eletricamente neutra, é posta em contato elétrico com a segunda, com carga . Em seguida, é posta em contato elétrico com a terceira esfera, cuja carga vale . O campo elétrico produzido pela primeira esfera a uma distância de seu centro vale:

A) , apontando para fora da esfera

B) , apontando para dentro da esfera

C) , apontando para fora da esfera

D) , apontando para dentro da esfera

E) zero

Vamos imaginar a primeira interação, a esfera neutra encosta na esfera carregada com carga .

As esferas entram em equilíbrio de cargas e se separam, assim as cargas em cada uma será

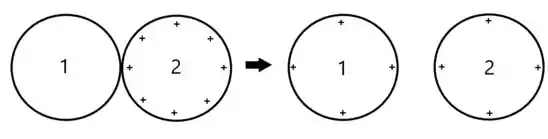
Dessa forma, como antes tínhamos as cargas e , agora ambas têm , concorda?

Agora na segunda situação, a esfera que agora está carregada com , encosta na esfera que está carregada com .

Assim, quando as esferas estiverem em equilíbrio, vamos ter

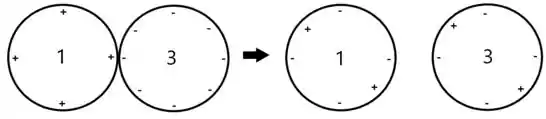
Portanto a carga final da esfera depois de todos esses processos é de .

Tudo certo até aqui? 👀👀

Agora vamos calcular o campo elétrico da esfera .

Para o campo elétrico externo às esferas, calculamos como

No caso, é a carga da esfera dada por e é a distância do ponto que queremos observar até o centro da esfera, ou seja

Substituindo esses valores em

Simplificando o resultado

O que é , a constante eletrostática também pode ser escrita como , ou seja

Vamos interpretar nosso resultado, o campo elétrico no ponto que queremos é dado como e o sinal de indica que o campo está voltado no sentido oposto a , ou seja, voltado para dentro da esfera.

Analisando as alternativas do enunciado, vemos que a alternativa B) é a que descreve o resultado que obtemos!

É isso! Essa resolução te ajudou? Responde Aí! ✌