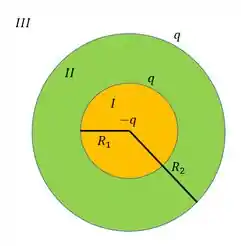
Uma esfera isolante maciça de raio está carregada com uma carga . Ela é circundada por uma casca esférica concêntrica, condutora, de raio interno e raio externo , que está carregada com uma carga de modo que a quantidade de carga na superfície interna é e na superfície externa é também.
Assinale a opção que especifica, corretamente o módulo dos campos elétricos nas regiões (), () e ()
- ; ;
- ; ;
- ; ;
- ; ;
- ; ;
Passo 1
- Região ()
Vamos escolher como superfície gaussiana uma esfera de raio . Pela lei de Gauss temos
Como o campo é radial temos
A carga total dentro dessa esfera de raio será
Como a esfera é uniformemente carregada
Já a densidade de carga é dada por
Assim
Voltando para o campo elétrico
Passo 2
- Região ()
O campo na região é o campo no interior da casca esférica. Como dentro de um condutor o campo tem de ser nulo temos
Passo 3
- Região ()
Vamos escolher como superfície gaussiana uma esfera de raio . Pela lei de Gauss temos
Como o campo é radial temos
A carga total dentro dessa esfera de raio será
De forma que
Resposta
(A)