Uma pequena esfera oca condutora, com raio interno e raio externo , é concêntrica com uma grande esfera oca condutora, com raio interno e raio externo , como mostra a Figura abaixo. A carga total sobre a esfera oca interna é igual a e a carga total sobre a esfera oca externa é igual a . Considerando que o sistema está no equilíbrio eletrostático,
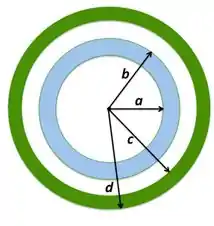
a) Determine o módulo, direção e sentido do campo elétrico em função de ao centro comum para as regiões
- ;
- ;
- ;
- ;
b) Qual é carga total sobre
- a superfície interna da esfera oca pequena;
- superfície externa da esfera oca pequena;
- a superfície interna da esfera oca grande;
- a superfície externa da esfera oca grande?
Passo 1
a) Como ambas as cascas são condutoras, fica mais fácil analisar como fica o campo elétrico em cada região. Por exemplo, como a casca condutora menor tem uma carga positiva de , o campo elétrico em toda a região é nulo, já que toda essa carga vai para a superfície da casca condutora menor.
i) e ii) Portanto, tanto para , quanto para , o campo elétrico é nulo, ou seja, .
iii) Agora, dentro da região , existe a carga que está sobre a superfície da casca esférica menor. Portanto, o campo nessa região é idêntico àquele que seria produzido caso a carga estivesse localizada no centro da Figura. Por isso,
Tranquilo??
iv) Continuando, a gente tem também uma outra casca esférica condutora de raio que possui uma carga total de . Mas, de novo, como é uma casca condutora, dentro dela na região não há campo elétrico, ou seja, para essa região.
v) Por último, na região , se fazemos uma superfície gaussiana esférica englobando as duas cascas, notamos que dentro dessa gaussiana há uma carga total de , que é a soma da carga da casca interna com a da casca externa. Por isso, o campo elétrico nesse caso é
Passo 2
b) Para o caso das cargas, como não há campo elétrico na região para então
- A carga elétrica é nula;
- Já na superfície externa da casca esférica menor, a carga é .
Agora, como a casca esférica maior tem uma carga total de e existe uma carga interna a ela na superfície externa da casca condutora menor, na superfície interna da casca esférica maior (em ) haverá, no equilíbrio eletrostático, uma carga negativa que será induzida pela carga que está na casca esférica menor. Blz?
Portanto,
iii) Carga elétrica negativa .
Por último, isso significa também que, na superfície externa da casca esférica maior haverá uma carga positiva . Só para confirmar, a carga total da casca esférica maior é , como deveria ser, correto? Então,
iv) Carga elétrica positiva de .
Resposta
a)
- ;
- ;
- ;
- ;
b)
- ;
- ;