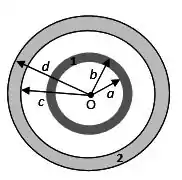
Duas cascas esféricas condutoras concêntricas e , têm a disposição indicada na figura abaixo. A casca tem raio interno , raio externo e está carregada com uma carga líquida . A casca tem raio interno , raio externo e está carregada com uma carga líquida desconhecida .
Medidas realizadas no sistema mostram que:
- o fluxo elétrico através de uma superfície gaussiana esférica de raio é igual a
- a densidade de carga na superfície externa da casca é igual a .
Com estas informações responda aos itens abaixo:
(a) Qual é o valor da carga líquida na casca ?
(b) Encontre o campo elétrico nas regiões e .
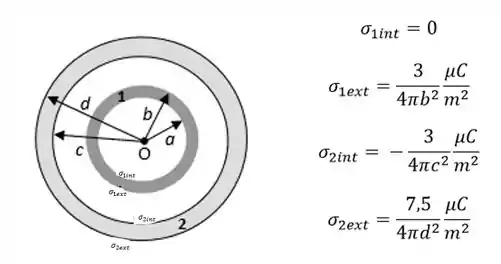
(c) Desenhe as cascas concêntricas e calcule (indicando também no desenho) as distribuições de carga nas superfícies internas e externas das duas cascas esféricas.
(d) Considere agora que no centro do sistema das cascas (ponto ) seja colocada uma carga puntiforme negativa de valor . Calcule o novo valor da densidade de carga na superfície externa da casca .
Passo 1
(a)
Sabendo que:
E que:
Devemos lembrar da definição de densidade superficial de carga:
Opa! Concluímos então que:
(A única carga presente na casca interna é a carga líquida que está na superfície externa)
Beleza, então como , temos que:
E então:
Mas, pela Lei de Gauss:
Voltando na equação anterior, e juntando as duas informações:
Passo 2
(b) As cascas esféricas são condutoras. Além disso, no interior da casca não há nenhuma carga. Portanto:
em
Para podemos usar Gauss. Considerando uma superfície gaussiana esférica de raio temos:
Onde é a carga envolvida pela superfície . Como o campo elétrico é constante em todos os pontos da superfície:
Mas
Passo 3
c)
Passo 4
Se no centro do sistema de cascas esféricas é colocada uma carga puntiforme o novo valor será de :
Caminhando de dentro pra fora, temos:
Já para dentro da casca 2:
E então, usando que:
Chegamos a:
Portanto:
Resposta
(a)
(b)
(c)
(d)