Duas esferas condutoras idênticas, muito pequenas, estão separadas por uma certa distância Originalmente, as duas esferas têm cargas de mesmo módulo e sinais opostos, e o módulo da força entre elas é , mantendo-se a distância, metade da carga de uma esfera é então movida para outra. O módulo da nova força entre as esferas é:
Passo 1
Bem, como de costume nosso aqui que tal começarmos fazendo um esqueminha dessas cargas?
Pelo enunciado, sabemos que são duas cargas em esferas pequenas separadas por uma distância . E elas têm a mesma carga em módulo (), mas de sinais opostos...
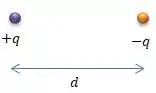
POW! De acordo com a Lei de Coulomb, então vai surgir entre essas cargas uma força de atração ...
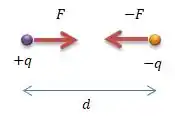
E o módulo dessa força que aparece de acordo com Coulomb é...
Onde significa módulo. Ora, o módulo das cargas é o mesmo, ou seja, , então...
Mas em um dado instante, a gente transfere metade da carga de uma para a outra! E aí? O que vai acontecer com a força? Venha comigo para saber
Passo 2
Cara, vamos supor que a gente pega a metade da carga da esfera negativa (laranja) e transfere para a azul...
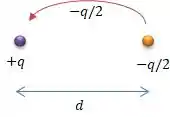
Cara, olha que doidera! Quando a carga chegar na azul com carga , a carga negativa que a gente acabou de inserir, vai neutralizar partes da carga positiva na esfera azul. E quanto de carga positiva que vai ser neutralizado?
Passo 3
Ora... Se estivermos inserindo , então a metade da carga positiva vai ser neutralizada, sobrando apenas na esfera azul...

A nova força que vai surgir entre as esferas será então pela Lei de Coulomb...
Porém, no passo vimos que a força antiga (antes de se passar metade da carga para o outro lado) era de ...
Então basicamente podemos falar que a força cai para da força original.
Resposta
Letra C