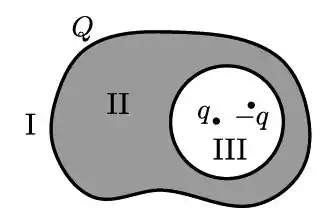
Um condutor, carregado com carga , possui uma cavidade esférica em seu interior. Nessa cavidade, há duas partículas, de cargas e . Chame de região o espaço fora do condutor, de região o condutor, e de região a cavidade. Qual das opções à seguir descreve corretamente o comportamento do campo elétrico nas três regiões?
Passo 1
Bom, já enchemos o saco a vida toda com esse assunto. Está na hora de você ser recompensado com um pontinho de graça (acredite, na sua prova vai cair uma questão idêntica, senão muito parecida).
Sabemos que no equilíbrio não pode haver campo num condutor em hipótese alguma, portanto:
Já eliminamos as alternativas e .
Passo 2
E o resto? Bom, nenhuma restrição com relação ao resto das regiões. No interior temos algo parecido com um dipolo. Como já vimos, o dipolo tem um campo ao seu redor sim. Nada de especial aí:
Daí eliminamos as alternativas e também, além da e da que já tinham sido cortadas. Só sobra uma alternativa, mas nós vamos brincar com a última região para efeito de estudo...
Passo 3
Analogamente, na região , temos o campo proveniente do dipolo mais o campo da carga contida no condutor (que vai ficar na sua superfície externa, lembra?). Portanto:
Resposta
Letra c