Uma barra de aço tem de diâmetro a . Um anel de latão tem um diâmetro interno de a . Se os dois objetos são mantidos em equilíbrio térmico, a que temperatura barra se ajusta perfeitamente o furo? Sabendo que o coeficiente linear de dilatação do aço é e o do latão é .
Passo 1
Temos inicialmente a seguinte situação para os dois materiais:
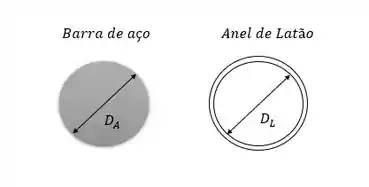
Ambos estão a e o diâmetro da barra de aço é maior que o diâmetro interno do anel de latão:
O problema quer saber em qual temperatura é possível acontecer isso aqui:
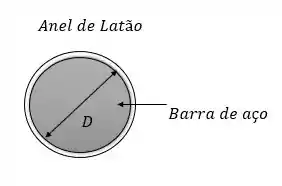
Ou seja, pra qual temperatura a barra de aço se ajusta perfeitamente ao anel de latão, e isso pra nós quer dizer que seus diâmetros finais devem ser iguais.
Como eles são mantidos em equilíbrio térmico eles estão sempre a mesma temperatura.
Como o problema quer que o tamanho final dos diâmetro sejam iguais, vamos igualar essas medidas para chegarmos no resultado que ele deseja.
Estamos avaliando a dilatação em duas dimensões, então vamos usar a equação da dilatação superficial aqui e encontrar uma relação pro diâmetro. E como estamos lidando com esse tipo de dilatação usaremos o coeficiente de dilatação superficial .
Lembrando que:
Como estamos analisando uma área circular temos o seguinte:
Substituindo:
Cortando os semelhantes temos:
Passo 2
Como falamos, o problema quer a temperatura em que o diâmetro final dos objetos seja igual, então vamos igualar as equações da barra de aço e do anel de latão e encontrar primeiro a variação de temperatura.
Assim podemos igualar
Onde :
E como:
Podemos então substituir os nossos dados na equação:
Atenção pra arrendondar só no final, hein!
Abrindo a expressão temos:
Isolando o
Arredondando:
Caso você arredondasse antes poderia rolar uma diferença de +- , portanto no caso de dilatação temos que levar várias constantes conosco já que a ordem de grandeza é muito relevante.
Passo 3
Descobrimos para qual variação de temperatura vai ocorrer o fato da barra e o anel terem a mesma área, mas o problema que a temperatura final e não a variação e por isso vamos fazer: