Como resultado de um aumento de , uma barra com uma rachadura no centro dobra para cima (figura abaixo). Se a distância fixa é e o coeficiente de dilatação linear da barra é , determine a altura do centro da barra.
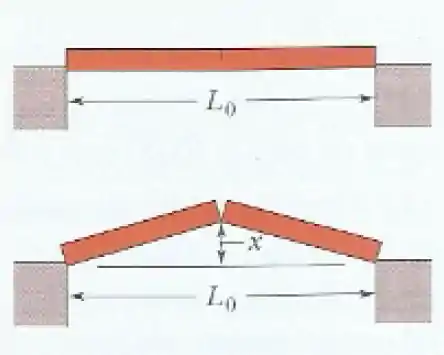
Passo 1
O problema quer saber a altura e para isso vamos precisar saber o tamanho final da barra, para que usando teorema de Pitágoras cheguemos na resposta.
Vamos lá então!
Passo 2
Para achar o tamanho da barra final, basta aplicar a equação que vimos na teoria
Como o problema forneceu todos os dados que precisamos, basta substituir na equação
Passo 3
Agora vamos fazer Pitágoras com uma das metades da barra quebrada, onde os dados são o seguintes
Com isso conseguiremos achar o valor da altura