Quando a temperatura de um cilindro é aumentada de pra , seu comprimento aumenta
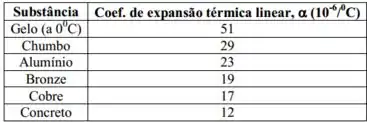
Com o auxilio da tabela abaixo, encontre de qual material o cilindro é feito.
Determine a variação percentual na densidade desse cilindro.
Passo 1
Bom, essa é tranquila: Basta a gente saber usar a formulinha abaixo:
Queremos saber o , pra assim determinar o material. Show?
Vamos lá:
O enunciado nos diz que o comprimento aumenta . Bom, isso quer dizer, matematicamente:
Sacou? O aumento equivale à variação. E essa variação corresponde à do valor inicial. Agora só falta a gente substituir ali a variação de temperatura:
Olhando na tabela, vemos que o material é o cobre.
Passo 2
Bom, aqui a gente passa a ter que lidar com grandezas e variações de volume. A fórmula agora é:
Onde:
Beleza, mas queremos saber da densidade, certo? A densidade é definida como:
Vamos chamar de a densidade inicial e de a densidade final.
Então:
O pulo do gato é saber a relação entre e . Bom, de acordo com a equação da variação, podemos escrever:
Então, se fizermos a razão entre e
Show?
Bom, agora só fazer aquela continha que esta ali embaixo, lembrando que
Ou seja, a densidade final cai pra da densidade inicial. Podemos dizer então, que a densidade do liquido variou
Resposta
Cobre