Uma barra homogênea com coeficiente de dilatação linear , mantida entre dois suportes rígidos com coeficiente de dilatação desprezível, é submetida a uma variação de temperatura T e, como resultado, se parte na sua metade, como mostrado na figura.
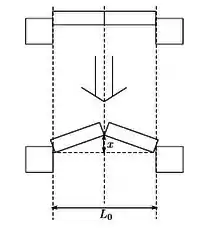
Considerando que a variação de temperatura é pequena quando comparada à temperatura inicial (), a altura x atingida pelo centro da barra pode ser escrita como:
a)
b)
c)
d)
e)
f)
Passo 1
A gente consegue resolver essa questão usando o Teorema de Pitágoras (isso mesmo, aquele dos triângulos retângulos). Dá uma olhada nesse triângulo aqui:
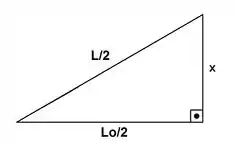
A barra se partiu porque dilatou. Então o comprimento da barra depois de partir é o comprimento final depois da dilatação.
Bom, a resposta tá em função de , então se acharmos acabou o problema.
Passo 2
Vamos usar a fórmula do comprimento final da barra em função da variação de temperatura e do coeficiente de dilatação linear:
E vamos aplicar o Teorema de Pitágoras:
Agora que vem o pulo do gato! Lembra que a questão disse que ? Isso quer dizer que a gente pode desconsiderar essa parcela com , porque ela será muito pequena. Então:
Resposta
Letra E.