Construir o gráfico da função definida em por:
Passo 1
Bom para fazer o gráfico de uma função modular a primeira coisa que temos que fazer é fazer aqueles módulos pela definição, e depois vamos somar os pedaços das funções.
Assim
A outra parte vai ficar
Passo 2
Agora é só jogar isso de volta na fórmula da função para fazermos isso direitinho. Antes disso, vamos entender os intervalos que apareceram. Vamos ter partes, uma menor que , outra entre e e outra maior que .
A nossa função vai ser
Temos que ir vendo como é cada função daquelas do módulo nos intervalos, vamos olhar uma coisa de cada vez
Começando com , aqui vamos ter, olhando a definição de módulo
Vamos ter, para
Passo 3
agora com , aqui vamos ter, olhando a definição de módulo
Vamos ter, para o nosso intervalo
Passo 4
Vamos para , aqui vamos ter, olhando a definição de módulo
Vamos ter, para o nosso intervalo
Passo 5
Agora que vimos as partes, vamos escrever a nossa função
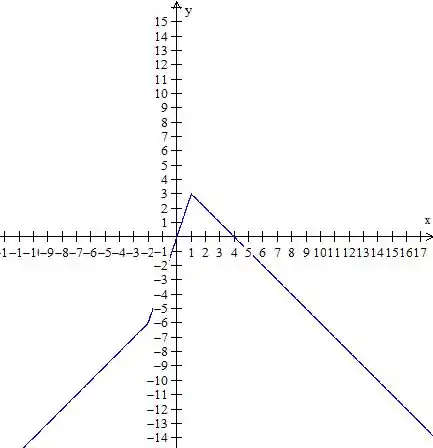
Temos funções de primeiro grau aqui, que são retas, então vamos pegar dois pontos em cada intervalo para fazer o gráfico,
Primeiro com
O gráfico dessa parte vai ficar
Lembra que temos que parar o gráfico em , mas o valor nesse ponto não entra na conta, por isso coloquei aquela bola aberta
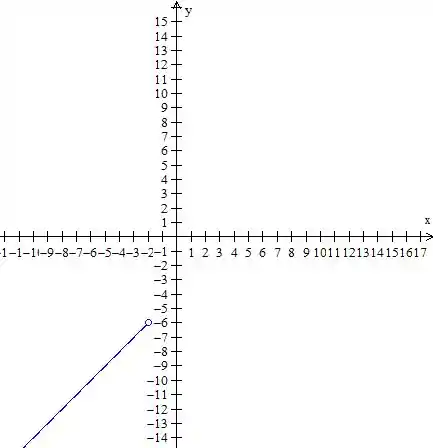
Agora com
O gráfico dessa parte vai ficar
Lembrando que aqui temos que incluir o valor do extremo em , mas excluir a parte em
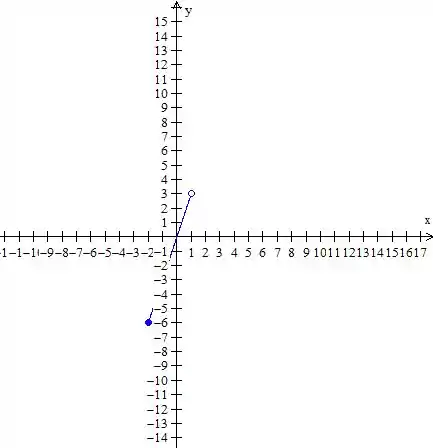
Para a última parte, onde , vamos ter
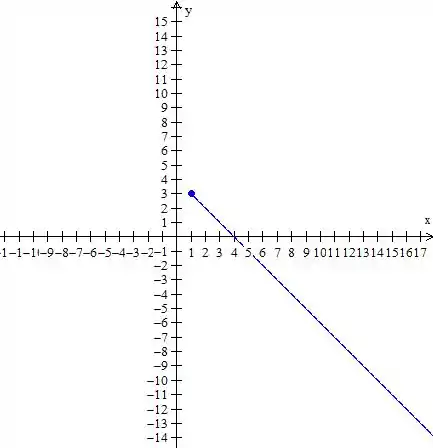
Agora é só desenhar tudo junto,
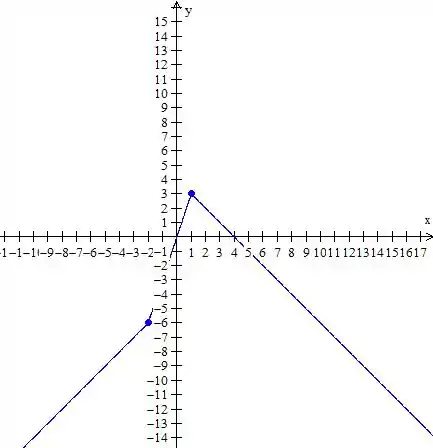
Essas “bolas fechadas”, como estão todas em cima da função mesmo, neste caso, não temos necessidade de deixar elas ali, se as funções não se juntassem nessa parte aí íamos precisar deixar, o gráfico fica
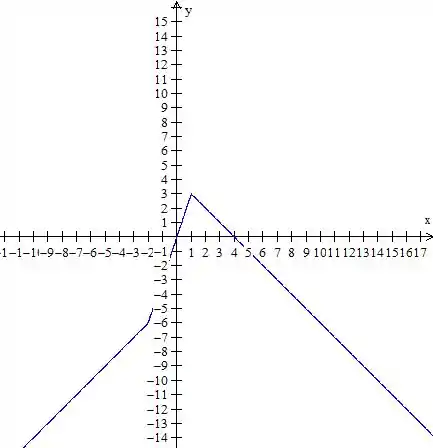
Resposta