Nos exercícios 31. a 46. Esboce o gráfico da função, especificando o domínio, a imagem e, quando possível, a paridade (par ou ímpar).
37.
Passo 1
Opa! Vamos começar avaliando o domínio dessa função
Para fazer isso, vamos ver onde que essa função pode dar problema. Vamos começar com o valor da função quando temos . Nesse caso
Como temos uma raiz, vemos a restrição que os termos dentro da raiz não podem ser negativos
Vamos resolver essa inequação
Então para essa função não ter problemas nessa parte, temos que ter . Só que como essa parte da função só tem essa cara () para valores de . Qualquer valor de nesse intervalo pode ser usado. Então, por enquanto não temos nenhuma restrição. Vamos para a segunda parte dessa função.Para temos
A restrição da raiz quadrada nos dá que
Então, para termos uma raiz quadrada de termos positivos, temos que ter , só que essa parte da função só tem essa cara para valores de e, de novo, não temos nenhuma restrição. Por isso, o nosso domínio é o conjunto de qualquer número presente nos reais, ou:
Passo 2
A imagem dessa função é só ver o que a gente tem como resposta quando pegamos os valores de dentro do domínio. Bom, como o domínio é qualquer número real, temos que olhar a cara da nossa função
Na primeira parte dela temos qualquer valor de que a gente coloque nessa raiz ela vai nos dar um número maior que zero, mas por conta daquele sinal de menos antes da raiz temos
Então para essa parte da função a nossa imagem vai ser
Falta agora olhar a outra parte . Dentro do domínio e do intervalo em que essa função está definida temos
Nessa parte da função temos a imagem
Agora a gente junta as imagens de cada parte e percebemos que se em uma a gente pega todos os valores da função que são negativos e na outra a gente pega todos os valores da função que são maiores ou iguais que zero, a imagem pode ser qualquer valor real:
Passo 3
Vamos agora ver como que é o comportamento do gráfico dessa função. Para fazer isso, vamos lembrar do gráfico de :
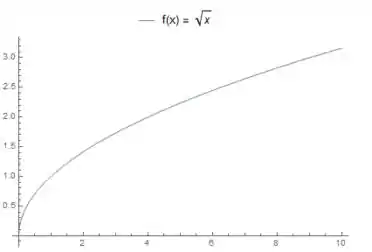
Vamos começar para valores . Nesse caso, a função que a gente tem que desenhar é
A primeira coisa que a gente pode reparar é que, em relação à função que a gente conhece , houve uma mudança no sinal de isso nos diz que é como se o gráfico inicial fosse espelhado ao longo do eixo . Assim, ó:
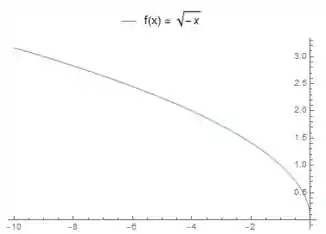
Beleza! Outra coisa que a gente percebe é que o nosso tá multiplicado por , isso só nos diz que os valores da nossa função vão aumentar um pouco
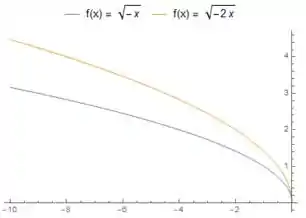
Bom, tudo que a gente fez foi pensando em mas no nosso caso, a gente teria que ter uma transformação do tipo que na prática é deslocar a função para a direita. Como temos o que a gente tem é que a função que a gente estava olhando tem que ser deslocada para a direita. Para saber aonde fica o inicio dela a gente tem que ver aonde ela zera
Então a gente desloca a função para ela começar em . Fica assim ó:
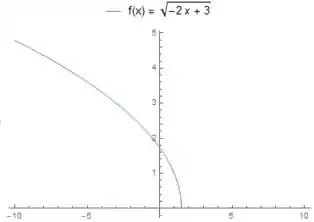
A última coisa que falta é que a nossa função é essa função que a gente acabou de construir o gráfico só que com um sinal de menos na frente . Isso é uma transformação do tipo e é como se a gente espelhasse a função em relação ao eixo . A gente tem então o gráfico para essa parte da função
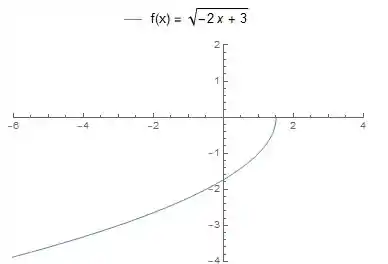
Como essa função está definida em . Ela deve ser aberta em .
Passo 4
Agora vamos ver o gráfico da função para . De novo, vamos pensar no gráfico de . A primeira diferença que a gente nota é que temos na raiz, ao invés de só essa mudança representa um aumento no gráfico em relação ao gráfico de :
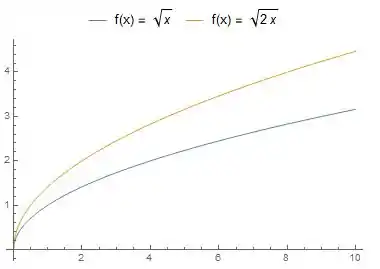
Uma vez que a gente sabe mais ou menos como o gráfico de deve ser, vamos pensar em como vai ser o de . Isso é uma transformação do tipo que na prática é como se a gente deslocasse o gráfico de para a direita.
Como temos o que a gente tem é que a função que a gente estava olhando tem que ser deslocada para a direita. Para saber onde fica o início dela a gente tem que ver aonde ela zera
Então o nosso gráfico fica deslocado para a direita, começando em . Então, para , o gráfico de deve ter essa cara aqui:
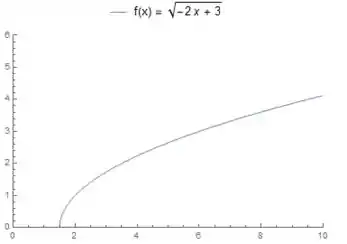
Passo 5
Agora vamos pegar alguns valores das nossas funções e usar a cara das funções que a gente acabou de ver para construir um esboço um pouco mais preciso.
Para : Sabemos que a função deve ser aberta em e nesse ponto, então vamos pegar alguns valores a partir desse ponto:

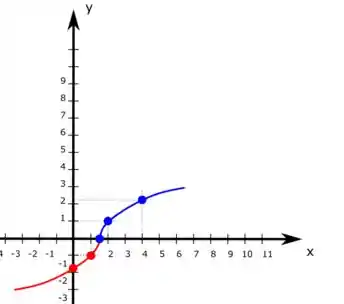
Usando esses valores no plano cartesiano e a forma da função nessa parte do gráfico, temos:
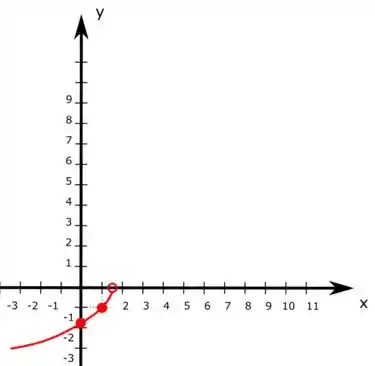
Para : Vamos pegar alguns valores a partir desse ponto:

Usando esses valores no plano cartesiano, juntando com o gráfico da outra parte e usando a forma da função nessa parte do gráfico, temos:
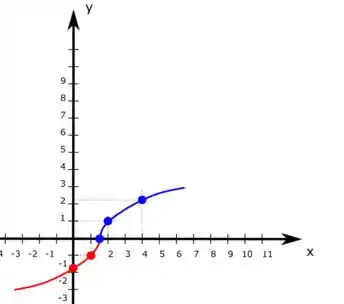
Resposta