Nos exercícios 31. a 46. Esboce o gráfico da função, especificando o domínio, a imagem e, quando possível, a paridade (par ou ímpar).
35.
Passo 1
Opa! Para fazer o gráfico de uma função modular a primeira coisa que temos que fazer é abrir aqueles módulos pela definição e depois vamos somar os pedaços das funções.
A outra parte fica
Passo 2
Agora é só jogar isso de volta na fórmula da função para fazermos isso direitinho. Antes disso, vamos entender os intervalos que apareceram. Vamos ter esses três intervalos aqui:
Isso nos diz que a nossa função vai ter três partes:
Nossa tarefa é usar esses intervalos nas definições dos módulos que a gente fez. Vamos começar com . Nesse caso a gente tem
Devolvendo esses resultados na nossa função temos
Passo 3
Vamos ver o intervalo de Nesse intervalo temos
Devolvendo esses resultados na nossa função temos
Passo 4
Vamos para . Olhando a definição do módulo temos
Devolvendo esses resultados na nossa função temos
Passo 5
Agora que temos o valor da função em todos os intervalos, a gente pode escrever
Essa função possui uma função constante () e 2 funções do primeiro grau, que são retas, então a gente precisa pegar dois pontos em cada intervalo para fazer o gráfico. Primeiro vamos olhar para . Apesar de não ser definido em vamos usar esse valor para estimar o gráfico e outro valor pode ser porque simplifica bastante:
O gráfico dessa parte vai ficar
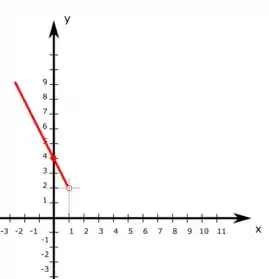
Agora, com temos a função constante que vai ser uma reta horizontal em . Assim, ó:
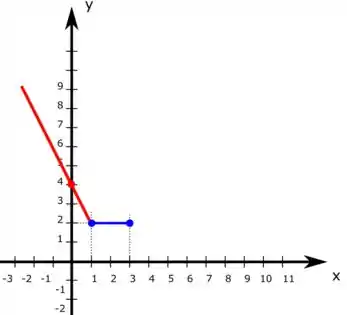
Por fim, vamos ver o que acontece em . Como é uma reta, temos que escolher dois pontos
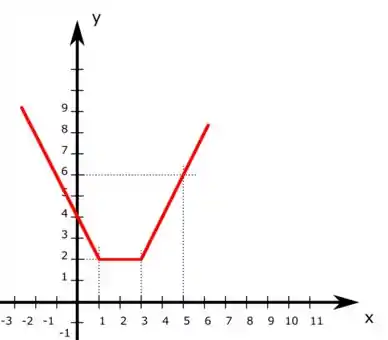
Marcando esses pontos no gráfico temos o nosso gráfico completo:
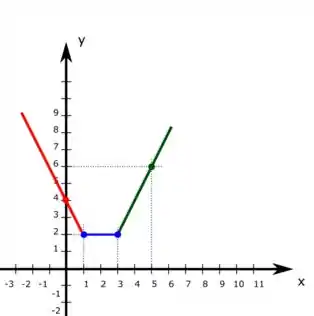
Resposta