UFF, Cálculo IA-Lista 1, GMA, 2008-1, 43
Esboce o gráfico da função, especificando o domínio, a imagem e, quando possível, a paridade (par ou ímpar).
Passo 1
Começando pelo domínio... A única restrição dessa função é o denominador, que não pode se anular:
Então o domínio de é .
Passo 2
Agora vamos entender melhor essa função analisando o sinal do numerador:
Passo 3
O gráfico de é uma parábola voltada pra cima com zeros em e , então temos:
Passo 4
Agora já podemos definir sem módulo:
Passo 5
Na verdade a boa vai ser aproveitar o fato que é uma raiz do numerador, e que tem aquele no denominador. Vê se eu não tô viajando:
Certo? Então:
Isso dentro do nosso domínio, porque devemos ter .
Passo 6
Ou seja:
Pra , a imagem de será
Para , a imagem de é
Para , a imagem de é
Assim dá pra ver que a imagem de é .
E esboçar vai ser tranquilo né?
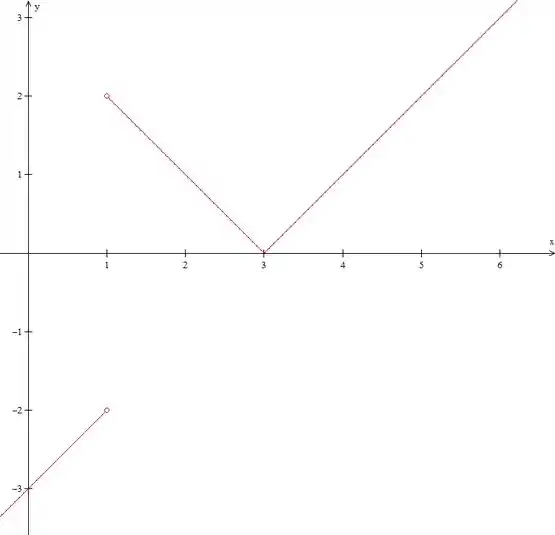
Com o gráfico podemos confirmar que não é nem par nem ímpar.
Resposta
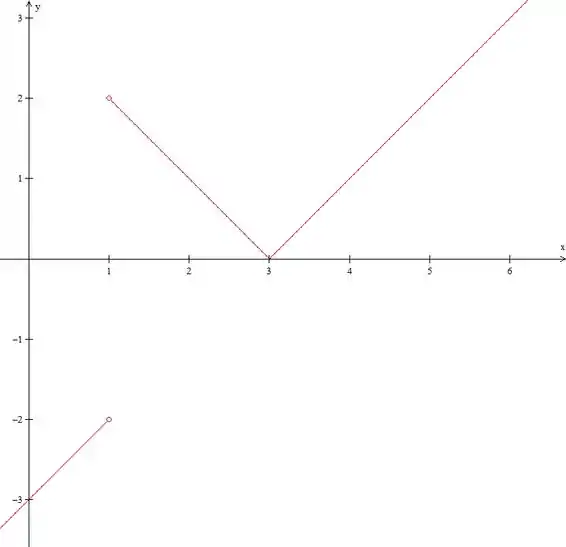
Não é par nem ímpar