UFF, Cálculo IA-Lista 1, GMA, 2008-1, 31
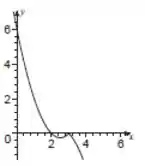
Esboce o gráfico da função, especificando o domínio, a imagem e, quando possível, a paridade (par ou ímpar)
Passo 1
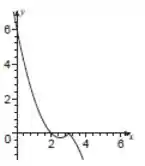Para esboçar o gráfico da função, basta substituir alguns pontos da função e ir marcando no plano cartesiano. Alguns pontos importantes são as interseções com os eixos. Nesse caso, o esboço do gráfico fica assim:
Passo 2
Agora vamos especificar o domínio e a imagem. Como se trata de uma função polinomial, não há restrições para o domínio, logo ele será:
Quanto à imagem, o jeito mais fácil de determina-la é olhando para o esboço do gráfico. Nesse caso, podemos ver que a função vai assumir todos os valores reais de . Portanto:
Passo 3
Finalmente, chegou a hora de verificar a paridade da função.
Resposta
Exercícios de Livros Relacionados
Encontre o domínio e esboce o gráfico da função: F x = 2 x + 1
Encontre o domínio e esboce o gráfico da função: g x = x x 2
1.45. Encontre o domínio e esboce o gráfico da função. G x = 3 x + | x | x
Esboce o gráfico:f (x) = |x + 1| - |x|
Esboce o gráfico:f (x) = ||x| - 1|