Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Função Modular

Ver Teoria
Exercício 7123456891011121314151617181920212223242526272829

Enunciado

UFF, Cálculo IA-Lista 1, GMA, 2008-1, 35

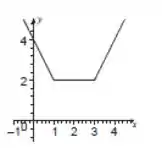
Esboce o gráfico da função, especificando o domínio, a imagem e, quando possível, a paridade (par ou ímpar)

f x = 3 - x + x - 1

Passo 1

x , como x = - 1 , x = 1 , x = 2 e assim por diante, até você perceber que o comportamento da função não irá se alterar mais. Feito isso, o esboço do gráfico fica assim:

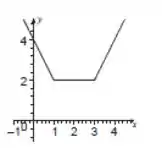
Passo 2

Vamos ao domínio e à imagem. Como é uma função modular com polinômios, o domínio será todos os reais.

d o m =   R

Quanto à imagem, pelo esboço do gráfico vemos que o menor valor que a função assume é 2 e que depois ela cresce infinitamente. Por isso

I m = [ 2 ,   + ∞ )

Passo 3

Só falta verificar a paridade da função.

f - x = 3 - ( - x ) + - x - 1 = 3 + x + - x - 1

f - x ≠ f x → F u n ç ã o   n ã o   é   p a r

- f x = - 3 - x + x - 1 = - 3 - x - x - 1

- f ( x ) ≠ f ( - x ) → F u n ç ã o   n ã o   é   i m p a r

Resposta

d o m =   R

I m = [ 2 ,   + ∞ )

Exercícios de Livros Relacionados

Encontre o domínio e esboce o gráfico da função: F x = 2 x + 1
Encontre o domínio e esboce o gráfico da função: g x = x x 2
1.45. Encontre o domínio e esboce o gráfico da função. G x = 3 x + | x | x
Esboce o gráfico:f (x) = |x + 1| - |x|
Esboce o gráfico:f (x) = ||x| - 1|