Esboce o gráfico da função, especificando o domínio, a imagem e, quando possível, a paridade (par ou ímpar)
Passo 1
Essa função dá aquela famosa tela azul na nossa mente né. Mas no fundo, ela não é tão tenebrosa assim. Primeiro, perceba que temos uma raiz quadrada elevada ao quadrado e essas duas operações se anulam. Portanto,
Muito mais simples né? Agora, pra analisar a função vamos dividi-la em duas partes:
Temos uma parábola com concavidade para cima se e uma parábola com concavidade para baixo se . Para ambas só há uma raiz, , e essa raiz coincide com o vértice. Com esses dados podemos esboçar seu gráfico.
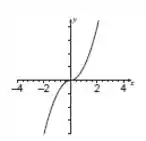
Passo 2
Não temos restrições ao domínio de , pois ela não possui denominador que pode se anular e também não possui valores que tornem a raiz quadrada negativo, por isso:
Quanto à imagem, pelo esboço do gráfico vemos que ela assume todos os valores de possíveis, portanto
Passo 3
Agora, veja que
Se
Então
E logo, podemos dizer com calma na alma que essa função é impar.
Resposta
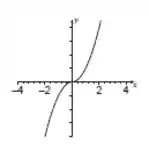
A função é impar